DWSIM Surrogate Model-Based Optimization
DWSIM Surrogate Model-Based Optimization
Goals
- Demonstrate a quick and flexible optimization framework using DWSIM models and their surrogates.
The article references a MATLAB executable notebook, code, and Simulink models found here.
High-Level Highlights
The surrogate model-based optimization framework leverages the speed and structure of surrogate models to provide quick and robust solutions to engineering optimization problems. We demonstrate this framework in the context of DWSIM models. The image below shows a typical result from the examples presented below. The surrogate model-based optimization can produce results in seconds (4.14 seconds), while a physics-based approach would take orders of magnitude more time (8416.99 seconds).

Surrogate Model-Based Optimization
In Surrogate Model-Based Optimization, we introduced an optimization framework that leverages the speed and flexibility of surrogate models to accelerate workflows. We demonstrated that the surrogate-based approach can solve constrained optimization problems in a fraction of the time compared to what a physics-based framework would require. This framework was the underlying engine that made computationally expensive workflows presented in Parameter Estimation via Profile Likelihoods and Anomaly Detection feasible. In the examples below, we again demonstrate the strengths of this framework through a series of optimization examples of a natural gas processing plant.
Surrogate Model
We refer the reader to DWSIM Surrogate Creation for a complete discussion of the natural gas processing surrogate model used here. The surrogate model’s inputs, outputs, and accuracy are all tabulated there.
Examples
The optimization examples focus on a DWSIM [1] model of a natural gas processing plant, aiming to minimize energy consumption while meeting defined constraints. Though simplified, these examples effectively demonstrate the framework’s ability to optimize objectives that depend on multiple model outputs.
To simplify the examples, we assume energy usage is computed directly from the duties of different equipment and is simply a sum of the duties. In reality, energy usage will depend on various factors, such as equipment efficiency. However, the examples demonstrate the surrogate model-based optimization framework can minimize an objective that is a function of several of the model’s outputs. The table below lists mechanical equipment included in the energy usage equation.
Users also have the flexibility to adjust the composition of the produced gas (the incoming gas into the system). As discussed in DWSIM Surrogate Creation, methane, ethane, and propane molar fractions of the produced gas are inputs to the surrogate model. However, each of these inputs has upper and lower bounds, and, in addition, the sum of these molar fractions must equal 0.8376 (to ensure a well-defined composition). Therefore, in the examples below, the user can adjust ethane and propane molar fractions while the methane molar fraction is computed based on the summation constraint (\( \text{x}_\text{methane} = 0.8376 – \text{x}_\text{ethane} – \text{x}_\text{propane} \)).
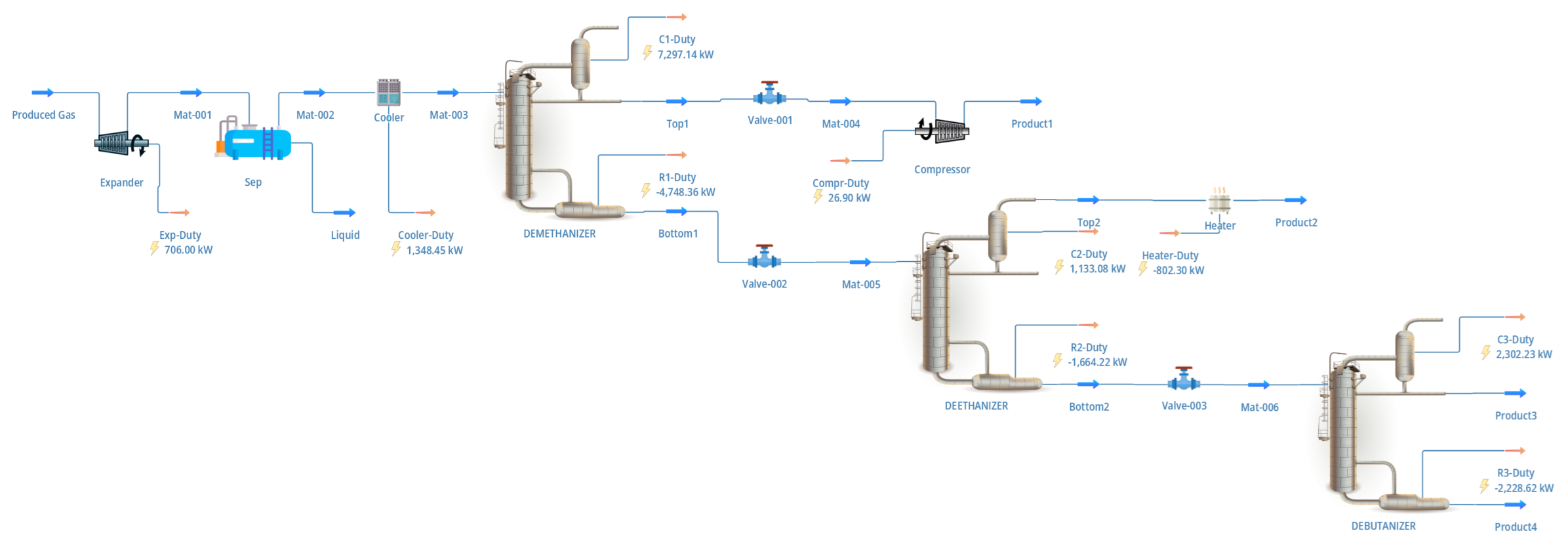
The image below displays a labeled flow sheet of the natural gas processing plant.
Example 1: Minimize Energy Usage
This example aims to determine the optimal operational settings that minimize energy usage while satisfying production constraints. The problem statement is summarized below:
\( \text{minimize Energy Usage} \)
\( \text{subject to} \)
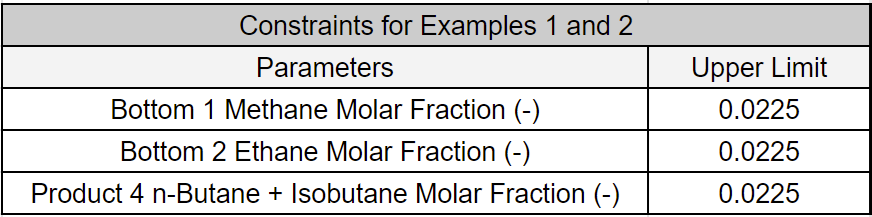
\( \text{Bottom1}_{\text{methane}} \leq 0.025 \)
\( \text{Bottom2}_{\text{ethane}} \leq 0.025 \)
\( \text{Product4}_{\text{butanes}} \leq 0.025 \)
The table below lists the decision and fixed variables of this optimization problem. For a discussion of the differences between decision and fixed variables, refer to Surrogate Model-Based Optimization.
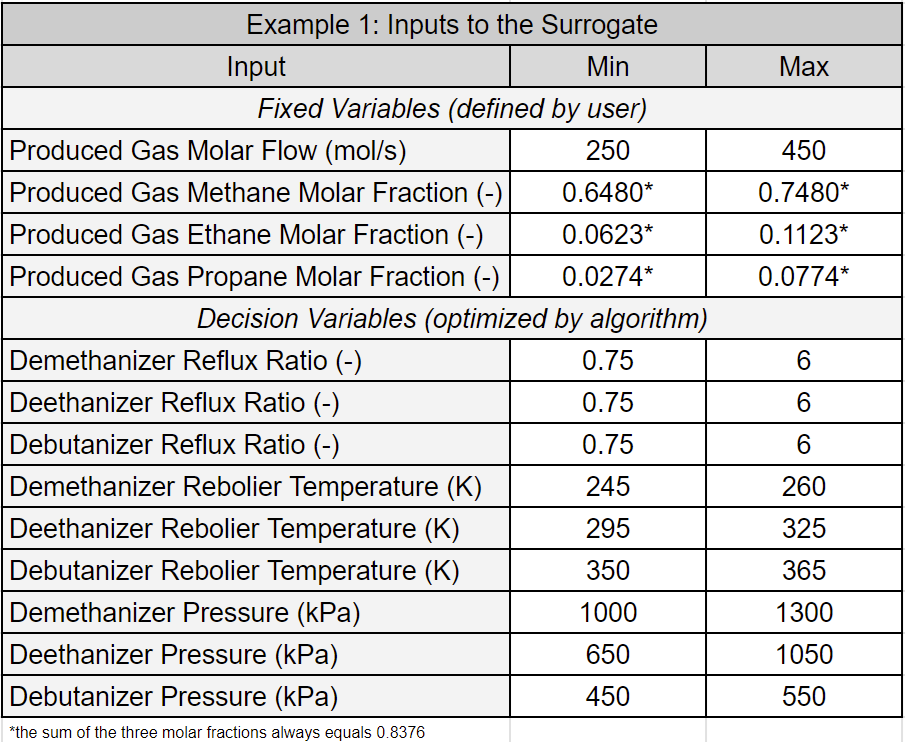
In the MATLAB executable notebook, users can adjust fixed variables and choose the number of optimization attempts. After setting these parameters, they can initiate the optimization algorithm by clicking the designated button.
The optimization process outputs a computational speed comparison between the surrogate model-based and physics-based approaches. It’s important to note the significant differences in computational time. The surrogate model-based optimization can produce results in seconds (4.14 seconds in the case shown), while the physics-based approach would take orders of magnitude more time. To ensure a fair comparison, we assume the physics-based approach will need the same amount of function evaluations. Furthermore, we use the average DWSIM execution time of the collected samples used for surrogate training.

The speed of the surrogate model-based optimization framework enhances existing workflows, offering users deeper insights into system performance. For instance, it can swiftly generate optimization curves, providing operators with a comprehensive view of optimal system behavior.
In the MATLAB executable notebook, users can efficiently compute the optimal operational settings and energy usage over a range of produced gas flow rates (while keeping the compositional fractions static). Using a surrogate model-based framework, users can create the plot below in less than a minute. In contrast, a physics-based optimization framework would require extensive computational resources and time to achieve comparable results.
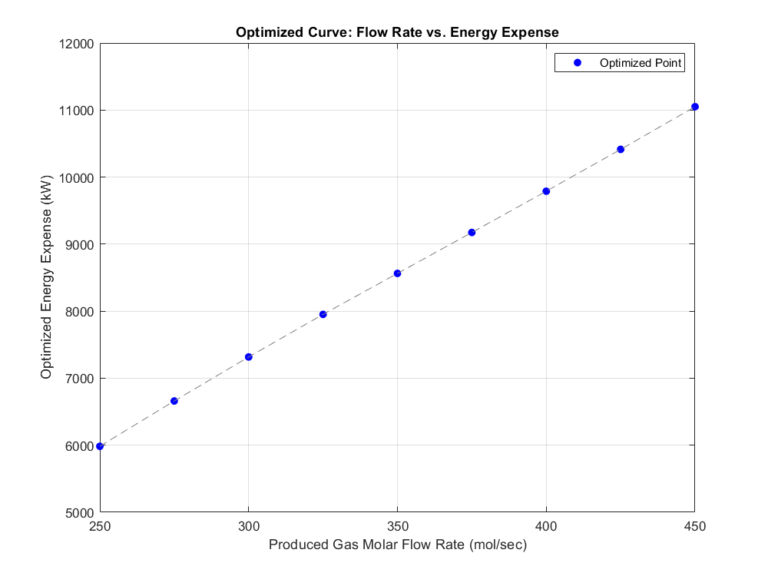
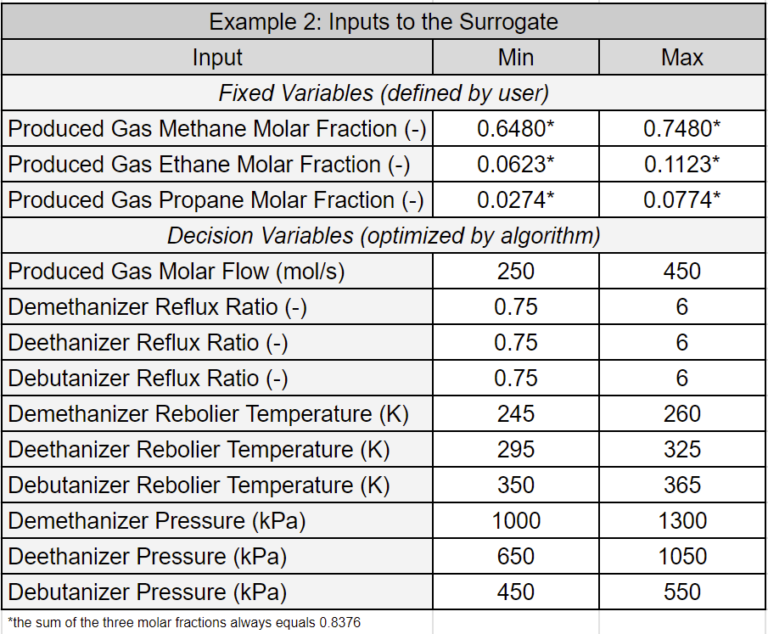
Example 2: Target Product 1 Flowrate
As in Example 1, this example aims to determine the optimal operational settings that minimize energy usage while satisfying production constraints. In addition to these constraints, the user defines a desired flow rate, \( FR_1\), for Product 1. The statement below summarizes the optimization problem:
\( \text{minimize Energy Usage} \)
\( \text{subject to} \)
\( \text{Product1 Flowrate} \approx FR_1 \)
\( \text{Bottom1}_{\text{methane}} \leq 0.025 \)
\( \text{Bottom2}_{\text{ethane}} \leq 0.025 \)
\( \text{Product4}_{\text{butanes}} \leq 0.025 \)
The table below lists the decision and fixed variables of this optimization problem. Unlike Example 1, the flow rate of produced gas is now a decision variable. For a discussion of the differences between decision and fixed variables, refer to Surrogate Model-Based Optimization.
In the MATLAB executable notebook, users can adjust fixed variables and choose the number of optimization attempts. After setting these parameters, they can initiate the optimization algorithm by clicking the designated button.
Note that the optimization framework successfully determined operational settings that achieve the desired Product 1 flow rate (within a small tolerance) while minimizing energy usage. Furthermore, similar to Example 1, the surrogate model-based optimization framework performs significantly faster than its physics-based counterpart.

Like Example 1, the surrogate model-based optimization framework enhances understanding of system behavior by leveraging its speed. In the MATLAB executable notebook, users can calculate optimal produced gas flow rates and energy usage across a range of desired flow rates for Product 1 (while keeping the compositional fractions static). Furthermore, leveraging the surrogate model-based framework makes this workflow quickly accessible.
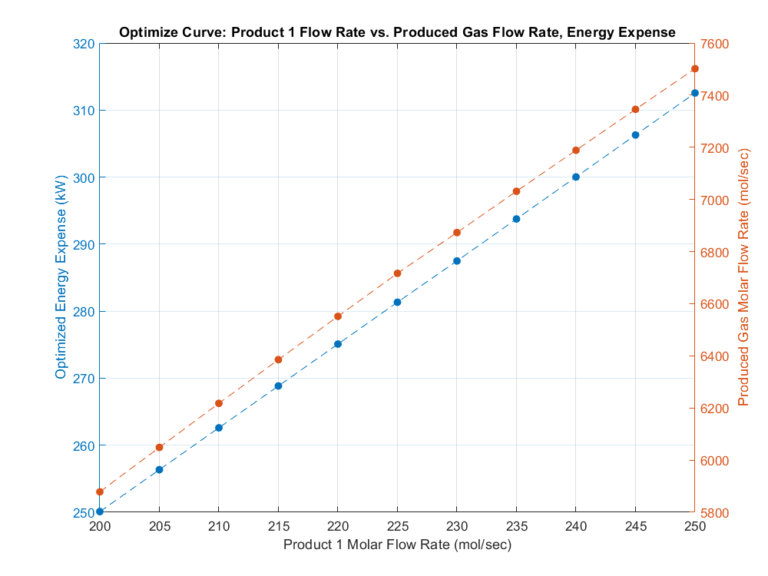
Example 3: Feasibility Study
In the final example, the user can define the operational molar fraction constraints (\( MF_i \)). However, some combinations of produced gas properties and operational constraints might be infeasible. Therefore, we perform a feasibility check before starting the optimization. This check ensures that the constraints can be met within the possible operational settings. If the constraints are feasible, the optimization proceeds in the same manner as the previous examples.
\( \text{minimize Energy Usage} \)
\( \text{subject to} \)
\( \text{Bottom1}_{\text{methane}} \leq MF_1 \)
\( \text{Bottom2}_{\text{ethane}} \leq MF_2 \)
\( \text{Product4}_{\text{butanes}} \leq MF_3 \)
The table below lists the decision and fixed variables of this optimization problem. For a discussion of the differences between decision and fixed variables, refer to Surrogate Model-Based Optimization.
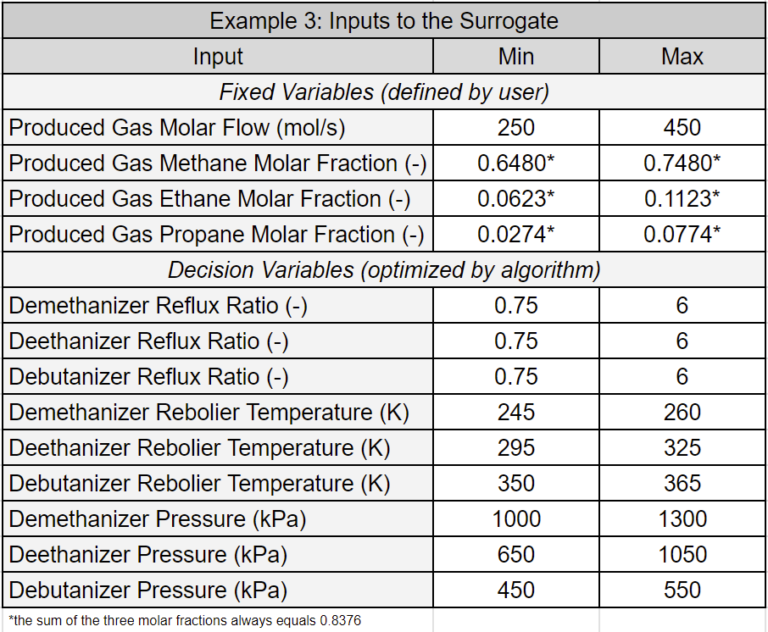
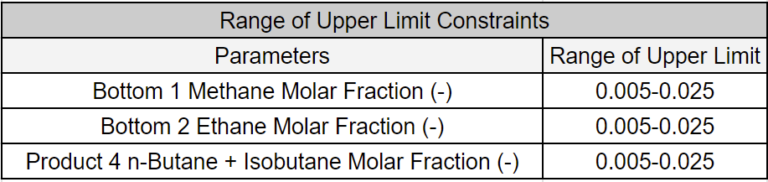
The table below outlines the range of constraints. It’s important to note that using a physics-based approach to prove the feasibility of an optimization problem can be computationally expensive, as the feasibility test requires numerous function evaluations (model executions). In contrast, a surrogate-based approach can quickly assess feasibility.
In the MATLAB executable notebook, users can adjust fixed variables, define operational molar fraction constraints, and choose the number of optimization attempts. After setting these parameters, they can initiate the optimization algorithm by clicking the designated button.

Summary
The DWSIM surrogate model-based optimization framework offers a robust and efficient solution for complex engineering problems. Using the speed and flexibility of surrogate models significantly reduces computational time compared to traditional physics-based methods. The optimization examples highlight its capability to meet strict production constraints and minimize energy usage. This innovative approach allows for deeper insights and rapid optimization, enhancing system performance and operational efficiency. Additionally, complex workflows such as Parameter Estimation via Profile Likelihoods and Anomaly Detection can be applied within the context of DWSIM.