Anomaly Detection
Anomaly Detection
Goals
- Anomaly Detection: Describe what anomaly detection is and its importance.
- Sampling and Data Comparison Methods: We present two approaches for anomaly detection, both of which leverage the speed and flexibility of surrogate models.
- Walk-Through: Offer a simple, step-by-step guide of an example using both approaches.
The article references a MATLAB executable notebook, code, and Simulink models found here.
High-Level Highlights
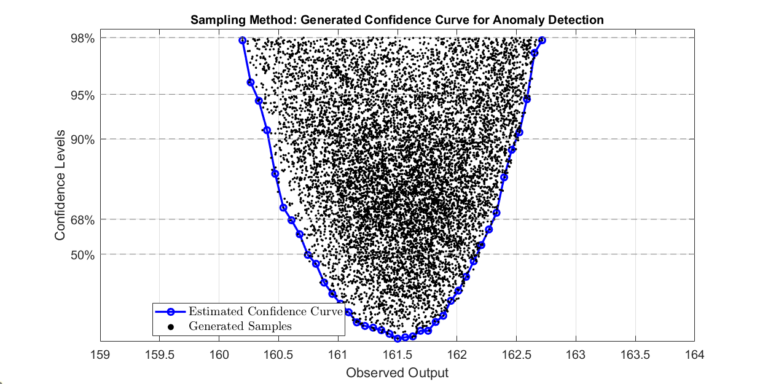
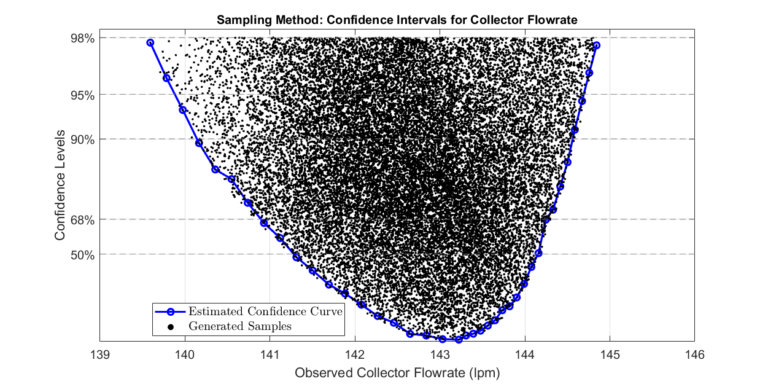
Quickly detecting anomalous events is essential for safety-critical or highly optimized systems. Anomalous events may give the first indication of a system fault, failure, or mode change. We present two methods for computing confidence levels of a model’s output. When used effectively, confidence levels can help you determine when an anomalous event occurs, thereby enhancing the safety and efficiency of systems. The plot below shows the result of the sampling method, a confidence curve of a system’s output. Both methods leverage the flexibility and speed of surrogate models to produce confidence curves quickly and robustly.
Anomaly Detection
Known and Uncertain Variables
Sampling Approach
Data Comparison Approach
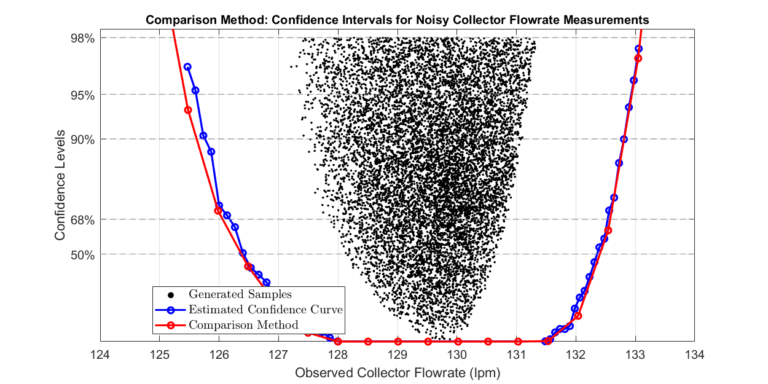
Sensor Noise
Example: Sampling Approach
Step 1: Estimate Unknown Model Parameters
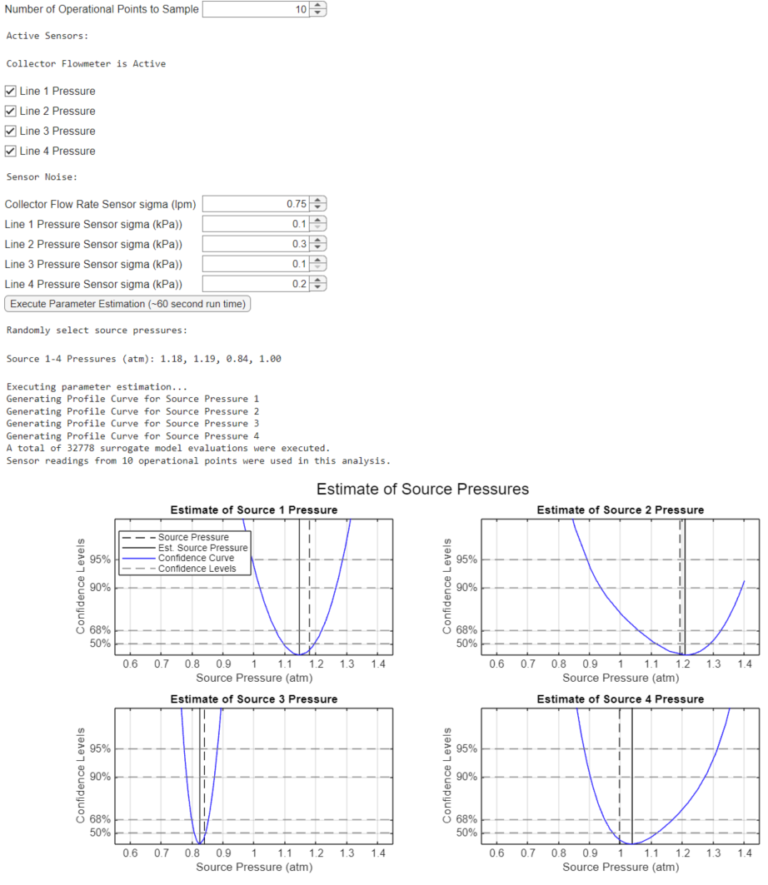
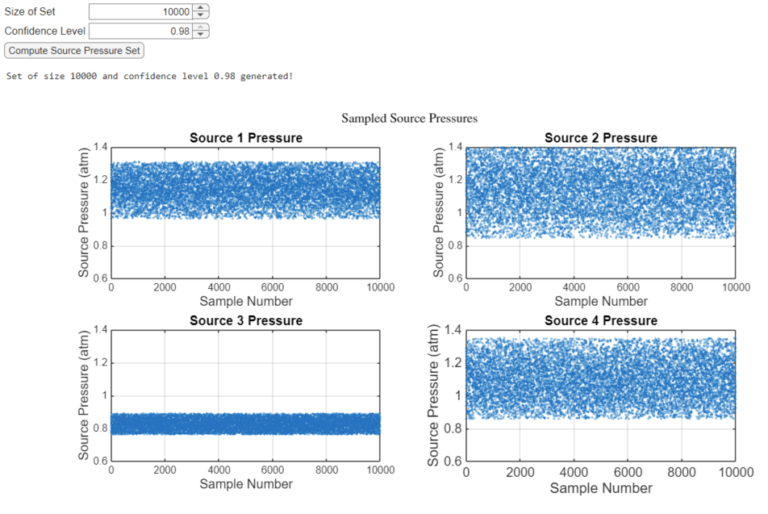
Step 2: Compute Source Pressure Set
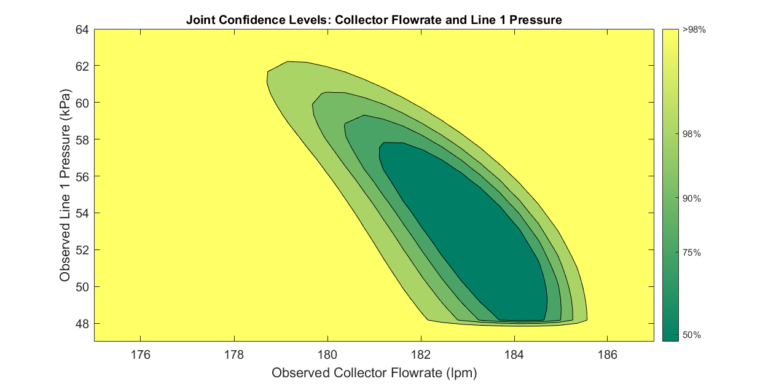
Once we compute the confidence intervals, a set \( \bar{P}_\alpha \) can be constructed. A set of the specified size is computed in which members fall within the specified confidence level. We plot the gathered set for visual inspection.
The image below captures the GUI and the output from the process.
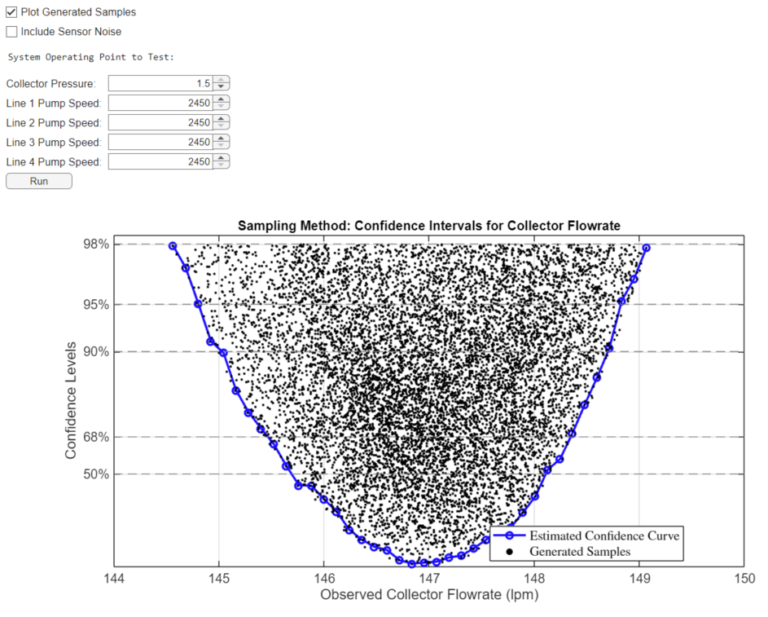
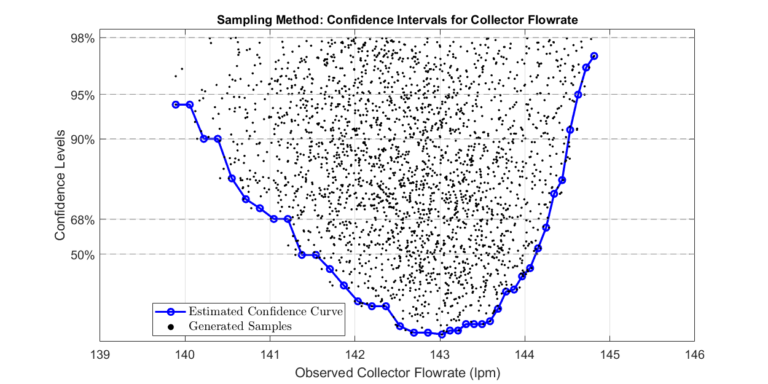
Step 3: Determine Confidence Intervals of Collector Flowrate
Example: Data Comparison Approach
Step 1: Collect Historical Data and Estimate Unknown Parameters

Step 2: Compute the Profile Curve of the Output
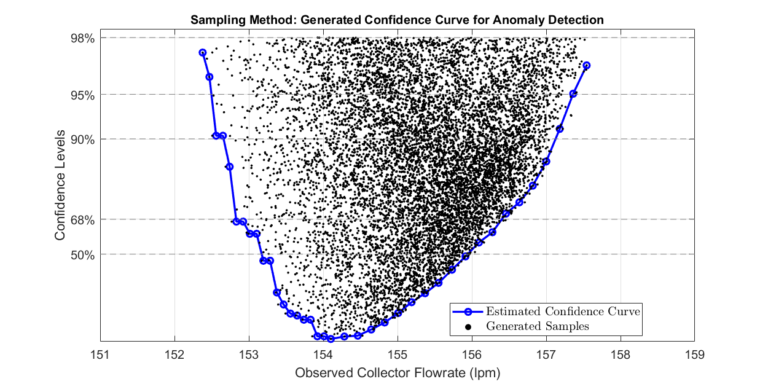
We use the historical data generated in the previous step to compute a profile curve of future collector flow rates.
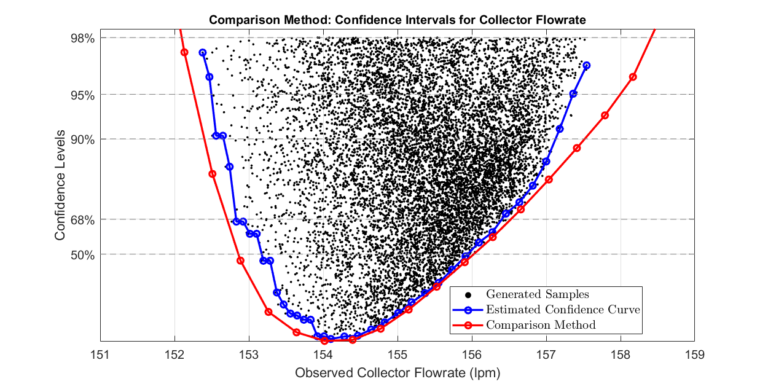
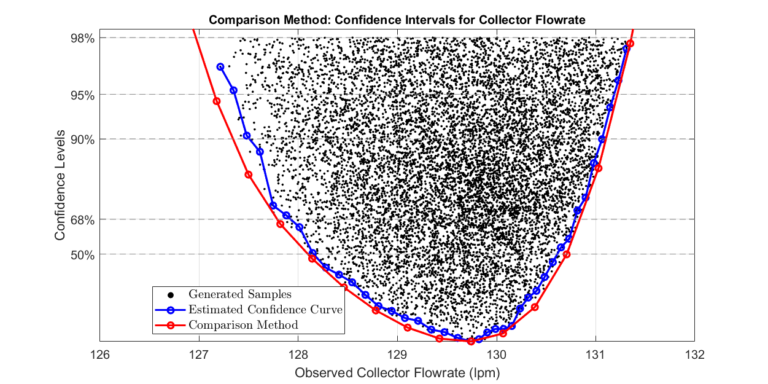
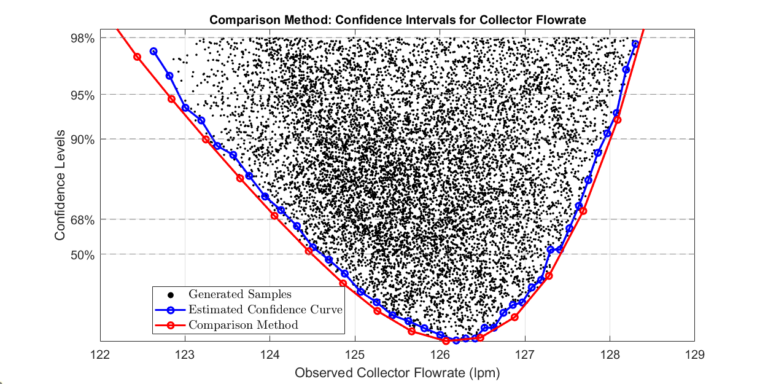
The plot compares the two approaches. Note that the comparison approach gives wider confidence bounds since the sampling method approximates confidence levels.
The MATLAB executable notebook provides a GUI where the user can define the operating point, select between different plotting options, and set the sampling set for comparison. The image below captures the GUI and the output from the process.
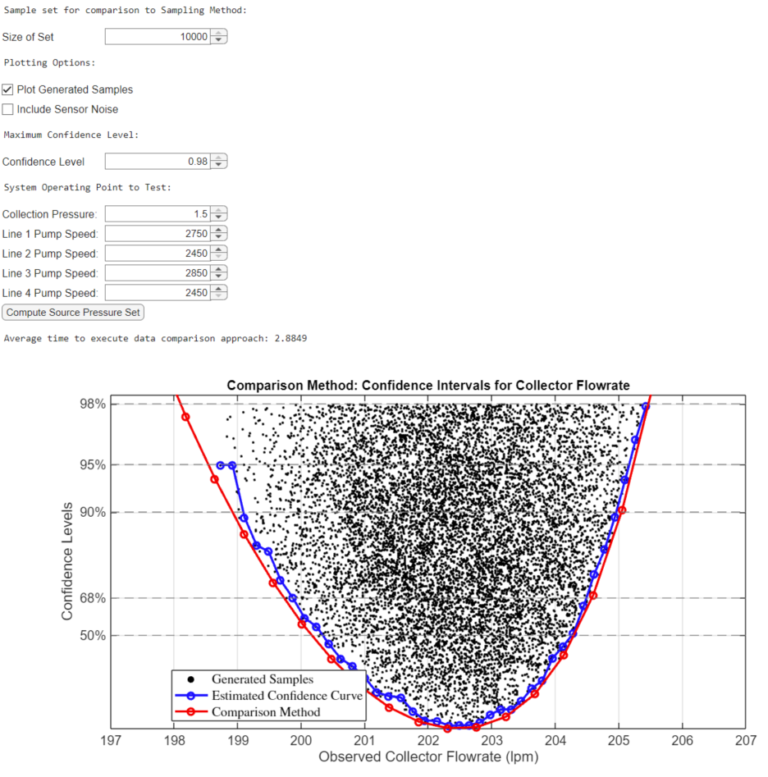
Results
Speed
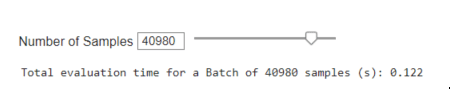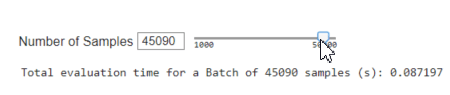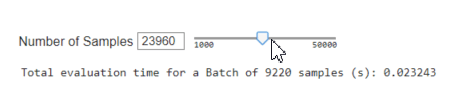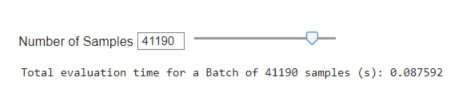
Including Sensor Noise
Sparse Samples
Asymmetrical Results
Multiple Outputs