Selective Sobol Sampling
Selective Sobol Sampling
Goals
- Discuss the Pitfalls of Passive Sampling: The Latin Hypercube and Sobol sampling algorithms do not consider existing information about the current data set or any previously trained models.
- Introduce Selective Sobol Sampling: Our proposed algorithm actively utilizes existing data and previously trained models to identify the most informative samples.
- Analytical Examples: Simple examples illustrate how Selective Sobol Sampling outperforms conventional methods.
- DWSIM Example: A chemical distillation column example demonstrates that SSS yields better surrogates.
The article references MATLAB code and data found here. The public repository omits the Selective Sobol Sampling algorithm. Please contact Gerardo De La Torre for details.
High-Level Highlights
We introduce the Selective Sobol Sampling (SSS) algorithm. A series of examples demonstrate that a surrogate model trained on data produced with the SSS algorithm results in lower prediction error metrics. The animated figure below shows the difference in convergence behavior for different sampling algorithms. We provide details of this experiment below. Since data is sampled more effectively, the computation time and cost to acquire a well-trained surrogate model are reduced.
Sampling Processes
The method used to generate input samples will significantly affect your surrogate model’s convergence rate, time to train, and performance. Sampling methods should get a complete and unbiased view of the system. Outputs are not distributed uniformly in nonlinear systems, and as a result, sampling methods may produce sparse samples in some regions of the output space.
Suppose the outputs of a nonlinear system are significantly skewed toward one region of the output space. In that case, the surrogate model will struggle to accurately predict the system’s behavior over the entirety of the output space. However, accurately capturing behavior over all regions may be critical for the surrogate model’s end use (parameter estimation, optimization, etc.). Figures provided in the first example below highlight this issue.
Latin Hypercube and Sobol Sampling
Latin Hypercube Sampling (LHS) is a statistical method that ensures a more uniform distribution of samples across the input space than simple random sampling [1]. By dividing each dimension into equally probable intervals and sampling from each interval, LHS guarantees that all regions of the input space are explored, which is particularly beneficial for capturing nonlinear relationships. However, the methodology used in LHS makes it cumbersome to add samples to an existing set [2]. Therefore, if the number of samples needed to train a sufficiently accurate surrogate model is unknown, LHS may not be ideal.
On the other hand, Sobol sampling is a form of quasi-random sampling that utilizes low-discrepancy sequences to fill the input space more evenly than random sampling [3]. This method is particularly effective in high-dimensional spaces, as it reduces gaps and clusters in the sample distribution, leading to better coverage of the input space. Due to the nature of the algorithm, an existing Sobal sample set can easily be expanded.
In the context of surrogate modeling, we classify both methods as passive. These methods do not incorporate information about the system or the structure of the surrogate model while generating a sample set or expanding a sampling set. Therefore, both methods may result in a skewed sample set.
Selective Sobol Sampling
Suppose we train a surrogate model with a data set generated from a physics-based simulator. However, the surrogate model does not meet specific accuracy criteria, and additional samples are needed to drive down its error. New samples will be determined passively if LHS or regular Sobol sampling methods are utilized. Instead, Selective Sobol Sampling (SSS) determines the best samples using information about the existing data set and a surrogate model trained on this set. The examples below illustrate how SSS can reduce prediction errors more quickly and uniformly than passive sampling methods. Therefore, SSS reduces the time and computational cost of generating a surrogate model.
Outline of the Selective Sobol Sampling Algorithm:
The Selective Sobol Sampling Algorithm is a prioritization algorithm since it ranks possible samples (a large input set) based on the information provided (existing data set and model). When updated information is available, the algorithm can re-rank the possible samples and provide a new set of selected input samples. The image below illustrates how SSS can be employed iteratively. The trained model and its training data set are used to select the next batch of model samples. A new model is then trained with the expanded set and warm-started with the existing model. If specified error criteria are not met, then another iteration is executed.
Selective Sobol Sampling does not require the existing data set to be of any type. Therefore, SSS can be used, for example, when a Latin hypercube sample set fails to meet performance requirements and additional samples are needed. This flexibility makes the algorithm a powerful tool when a well-fitted surrogate model is necessary.
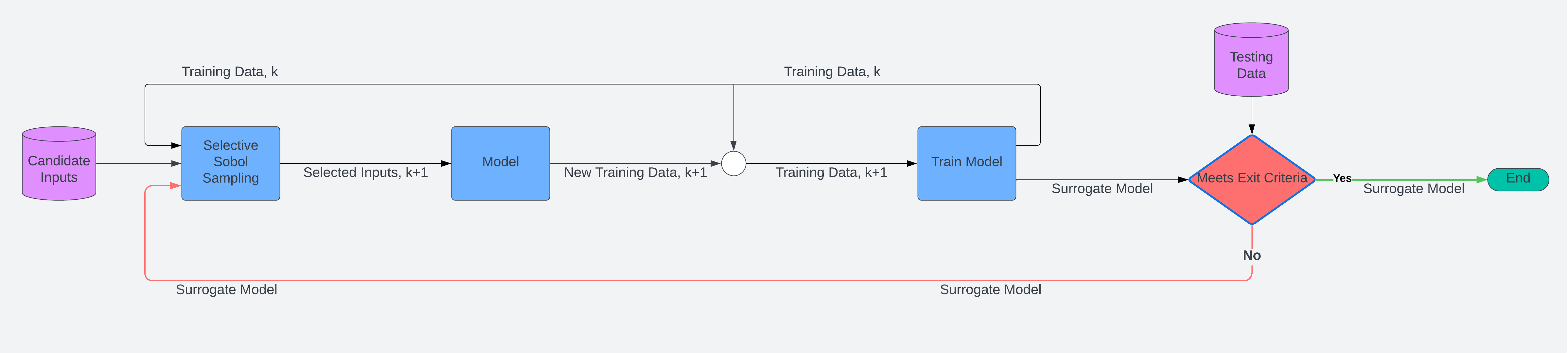
Summary of the Algorithm’s Inputs and Outputs
Inputs:
- Candidate Inputs: A large collection of potential inputs (examples below use a Sobol set of size 100,000)
- Current Training Data: The existing data used for training the model.
- Surrogate Model: A model trained using the current training data.
- Number of Input Points to Select: The desired quantity of input points to be chosen from the candidate set.
Outputs:
- Selected Inputs: A subset of the candidate inputs that have been chosen based on the algorithm’s criteria.
Experimental Setup
We conducted a series of experiments to illustrate the benefits of Selective Sobol Sampling. The experiments compare the performance of the surrogate model trained with different sampling algorithms. To ensure fair comparisons, we use the same testing data set (not used in training) to assess the maximum, mean, and standard deviation of a model’s prediction error for each sampling method. Furthermore, in each example, we use a common training algorithm, network size, and architecture. However, the Selective Sobal and Warm Start Sobal Sampling methods were warm-started with a previously trained surrogate model. The Analytical Examples section demonstrates warm and cold start Sobol sampling methods. Note there are minimal differences between these two Sobol methods.
Below is a brief description of each of the sampling methods.
Selective Sobol Sampling: The proposed approach creates input samples. If available, the network is warm-started with a previously trained surrogate model.
Warm Start Sobol Sampling: MATLAB’s sobolset function creates input samples. If available, the network is warm-started with a previously trained surrogate model.
Cold Start Sobol Sampling: MATLAB’s sobolset function creates input samples.
Latin Hypercube: MATLAB’s lhsdesign function creates input samples.
Random: MATLAB’s rand function creates input samples.
The associated MATLAB code and results for the following examples can be found here. Refer to the provided code for further details about each sampling method. The public repository omits the Selective Sobol Sampling algorithm and some results. Please contact Gerardo De La Torre for more information.
Analytical Examples
We first walk through a series of examples using straightforward equations as models to give an intuitive understanding of the benefits of SSS. In these examples, the “physics-based model” of the system is given by analytical expressions. Of course, one may think there is little benefit in using SSS if the computational expense of your model is very low. However, this may not be the case, as shown in the first example, where the quality (not the amount of the data) is the limiting factor in getting a well-fitted surrogate model.
These examples give an intuitive understanding of the approach and its potential benefits when more computationally costly models are used.
Motivating Example
In the first example, we demonstrate how SSS can shift the distribution of sampled outputs, leading to a better surrogate model with fewer samples.
Suppose we represent a system with the following equation:
\(y = \bigg(1 + e^{-(3x_1 + 2.8x_2 – 5.0)(10 + 48 \sqrt{(x_1 – x_2)^2})} \bigg)^{-1}.\)
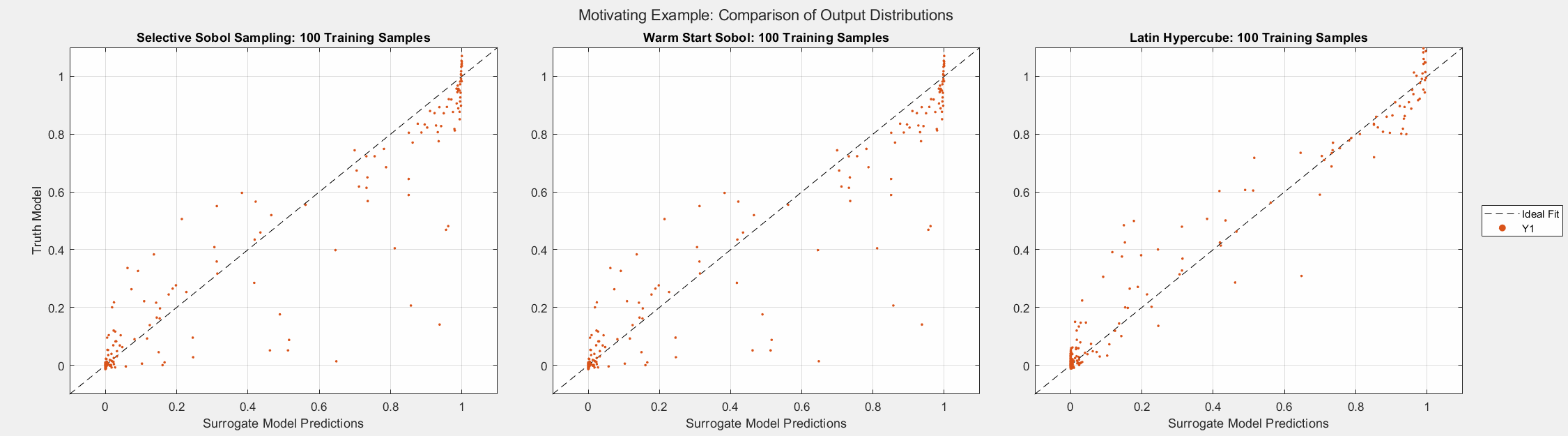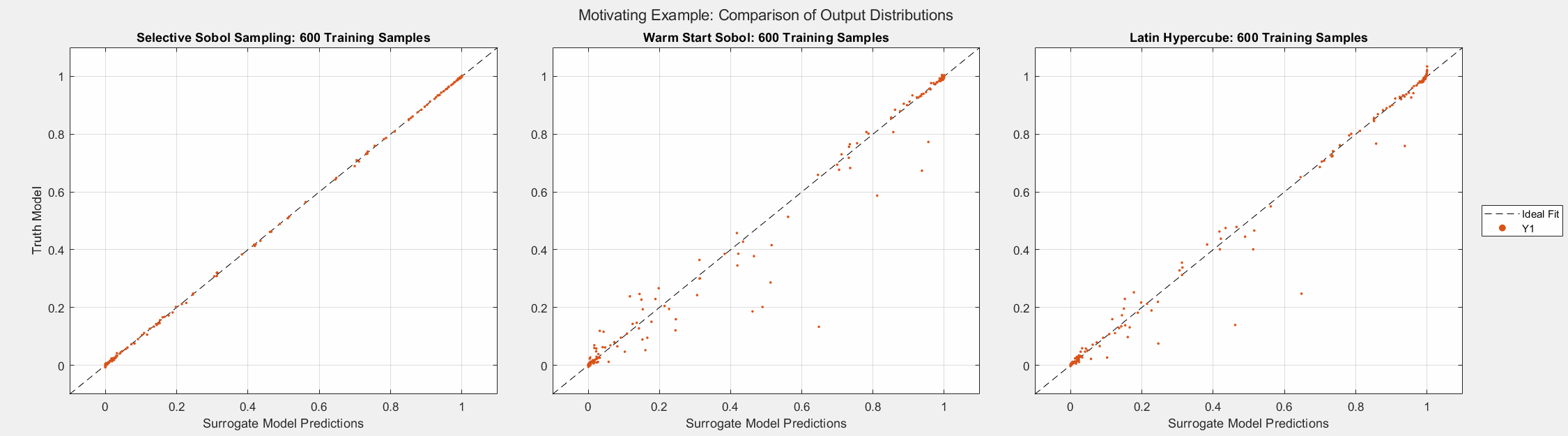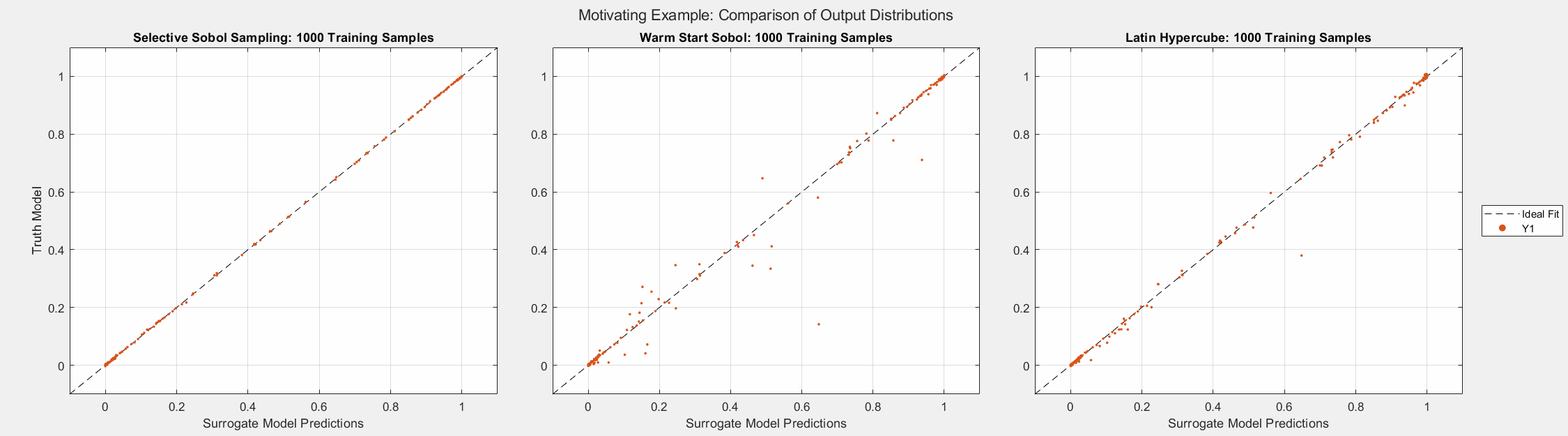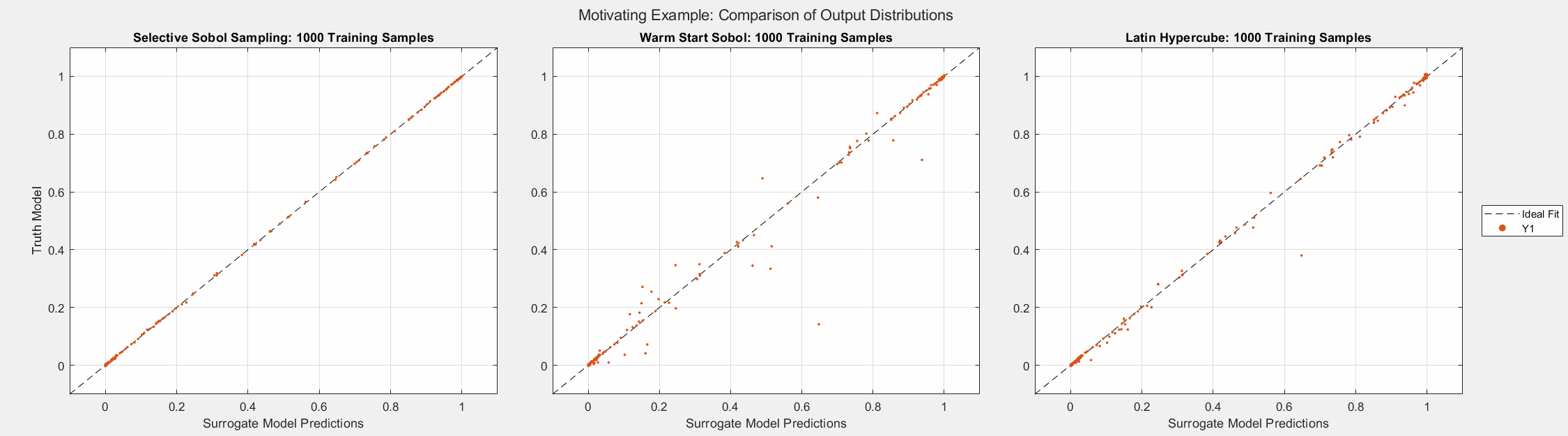
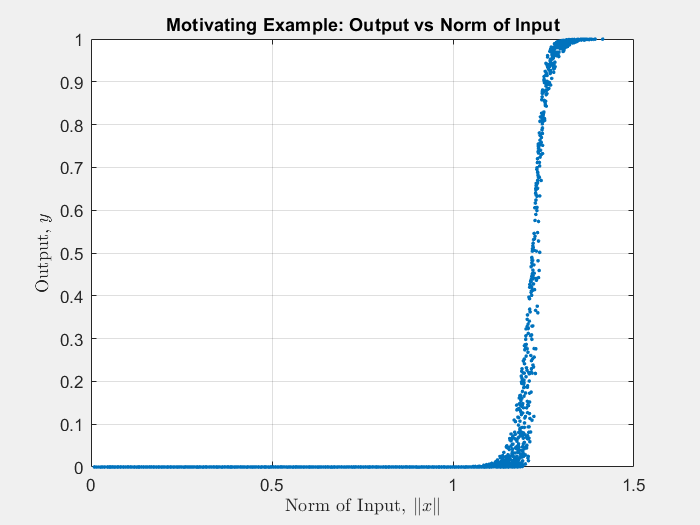
The figure below displays 10,000 random samples. Notice that most of the samples are near zero, and there is a sharp transition as the norm of the input increases. Therefore, as shown by the animated histograms, passively sampling this system will result in output samples mostly near zero. Therefore, it will be difficult for any passive sampling approach to generate a non-skewed data set. However, the samples generated by the SSS algorithm are less skewed, and the transition between 0 and 1 is better represented.
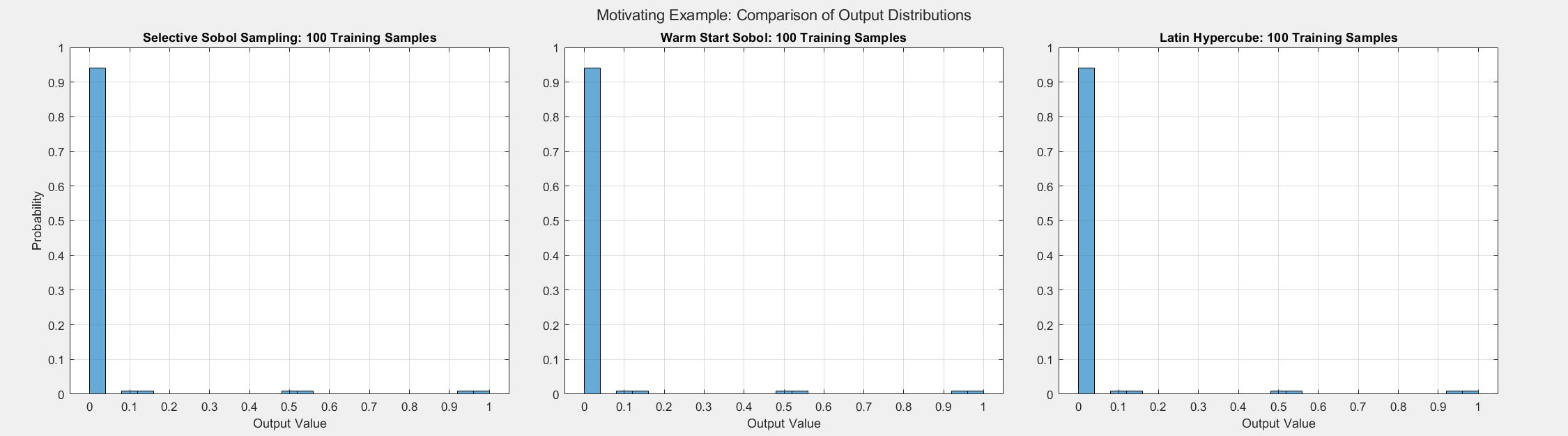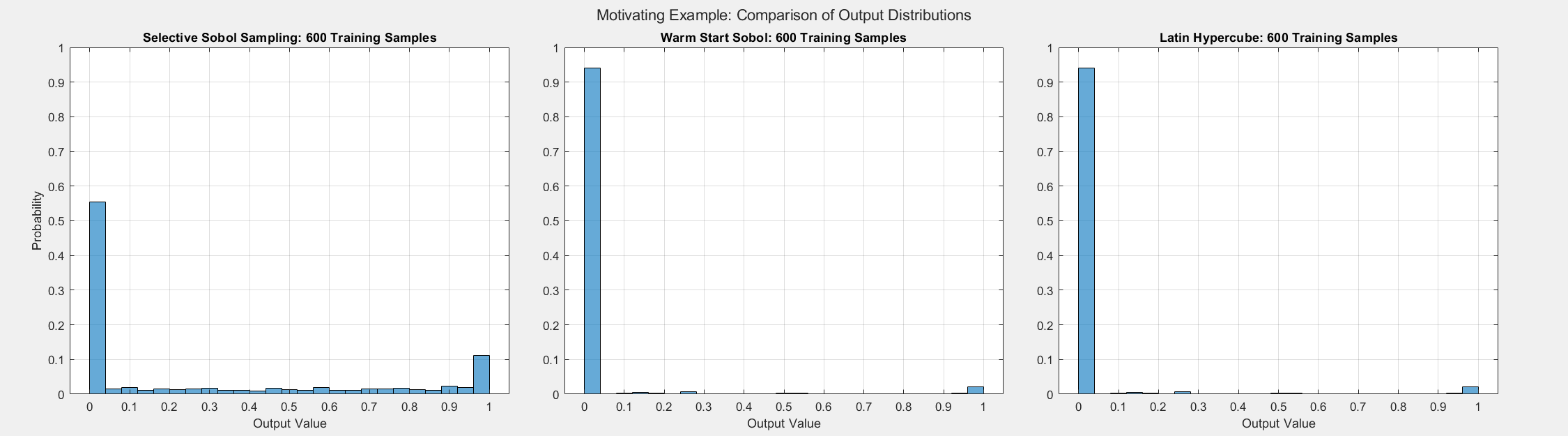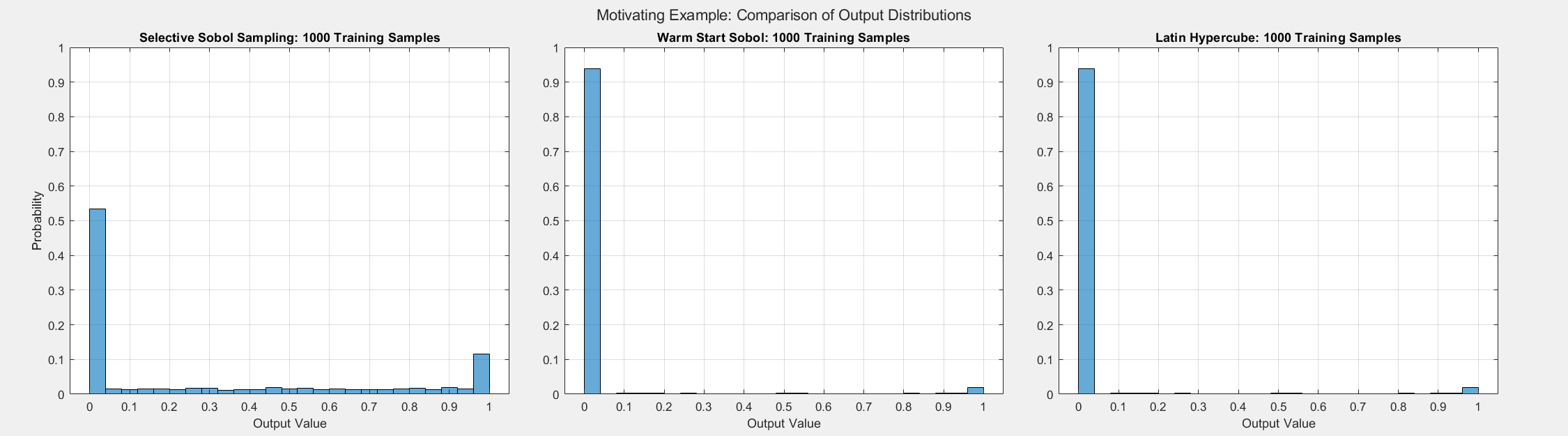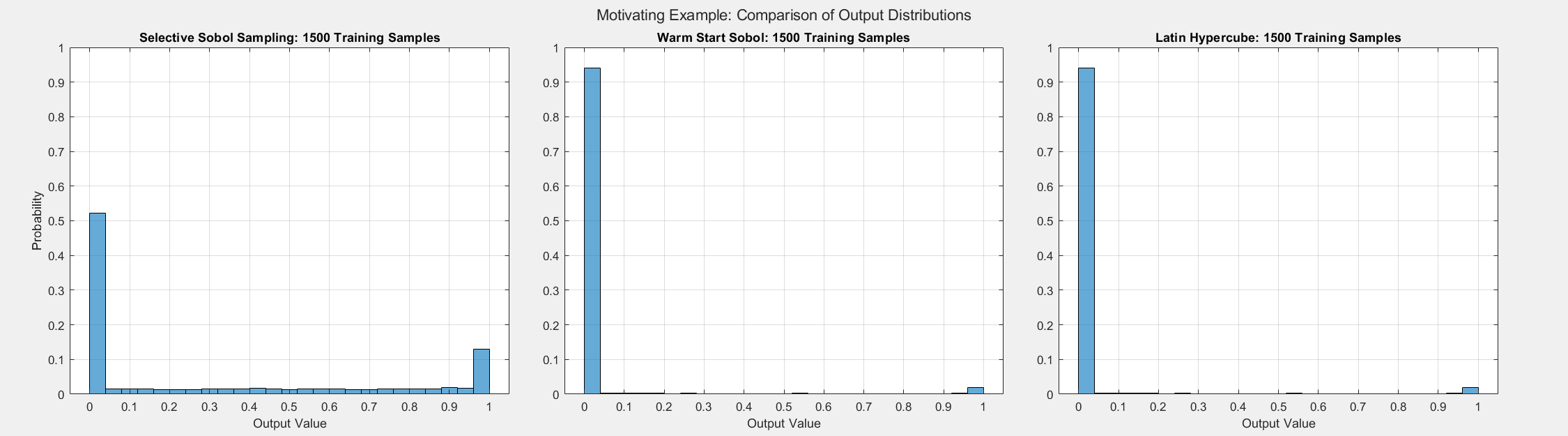
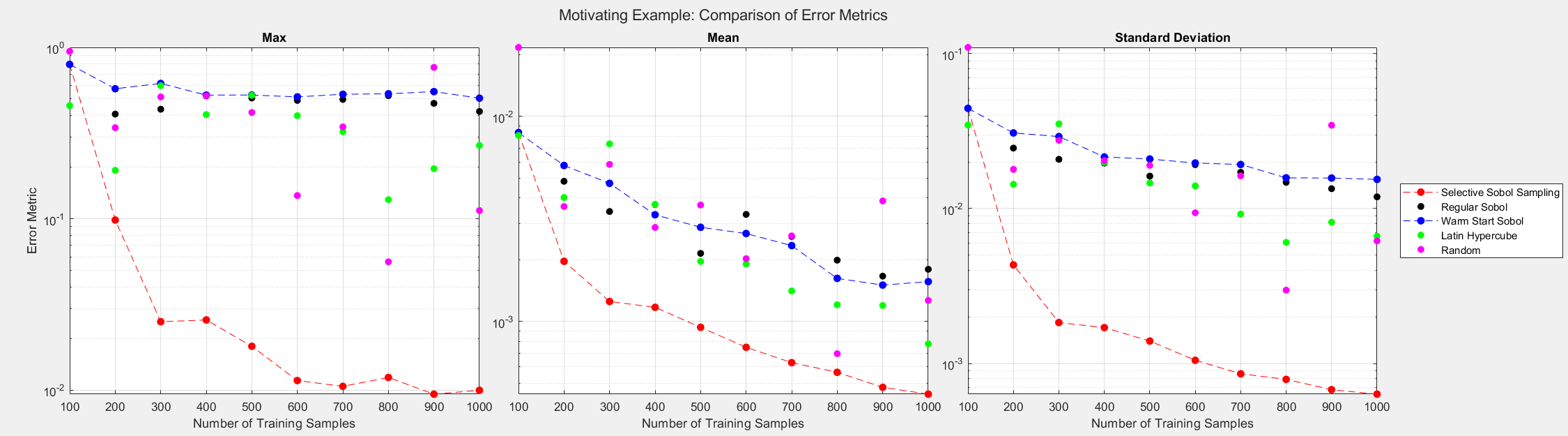
The figures below show the surrogate model’s convergence behavior when using different sampling approaches. We used the same testing set (2000 samples) to evaluate all metrics presented; see the associated code for details. Warm start sampling approaches are displayed with dotted lines to indicate dependence on a previous model. Sample sets were incremented by 100. See the provided code for details on the model architecture and training methods. SSS outperforms all passive sampling methods and consistently reduces the error metrics as more samples are used.

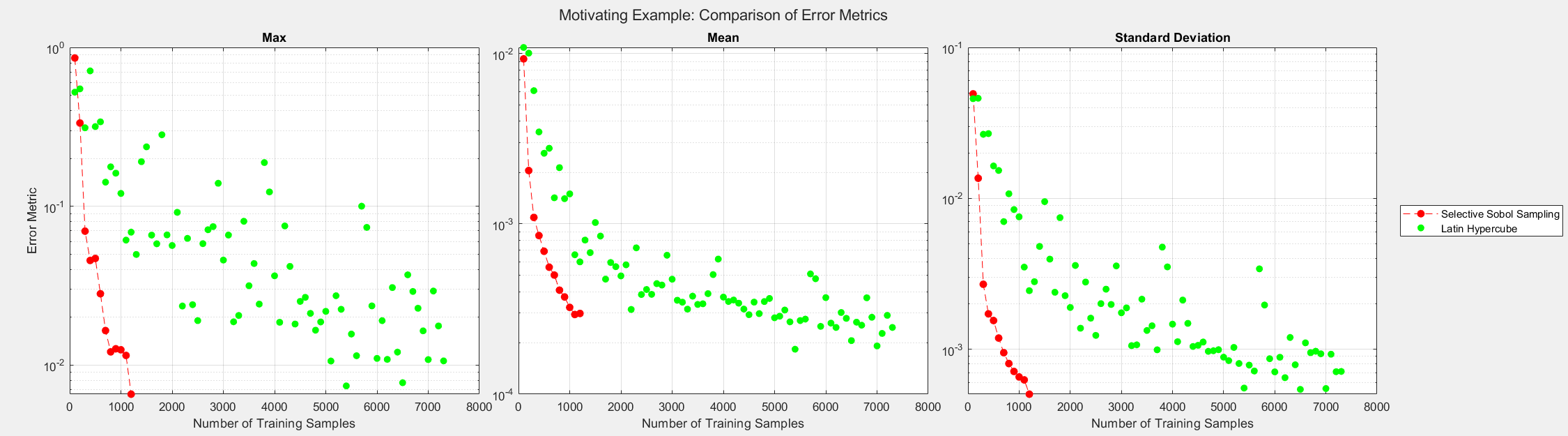
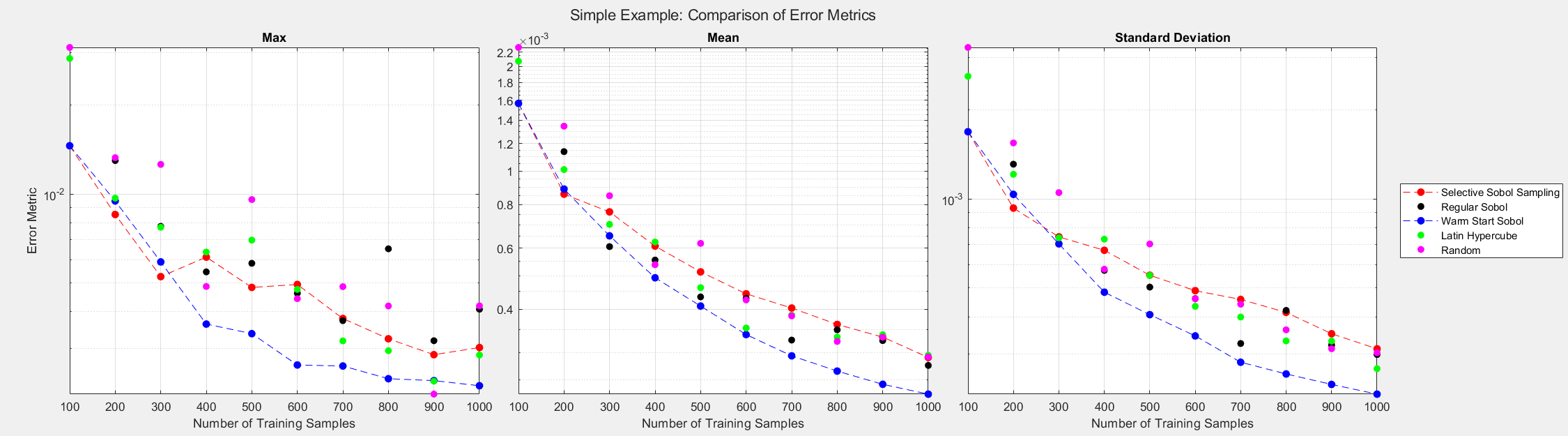
Quality, Not Quantity
Suppose an optimization use case requires the surrogate model to have a maximum error of 0.01. We can rerun the experiment to determine the data needed by Selective Sobol Sampling and Latin Hypercube algorithms to meet this requirement. The figure demonstrates that the Latin Hypercube sampling method requires more data to achieve the desired prediction accuracy. Furthermore, the Latin Hypercube sampling method is unpredictable, and predicting the maximum error for a given set size is difficult. The figure suggests a data quality issue, not a data quantity issue. Nevertheless, SSS can consistently drive the error metrics down as more data is added to the training set.
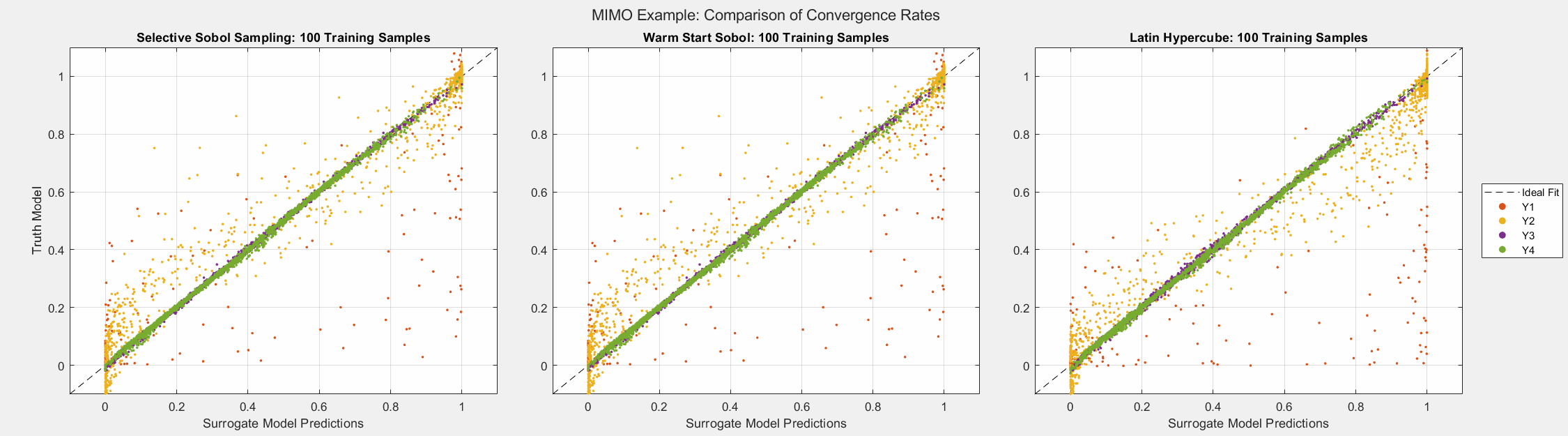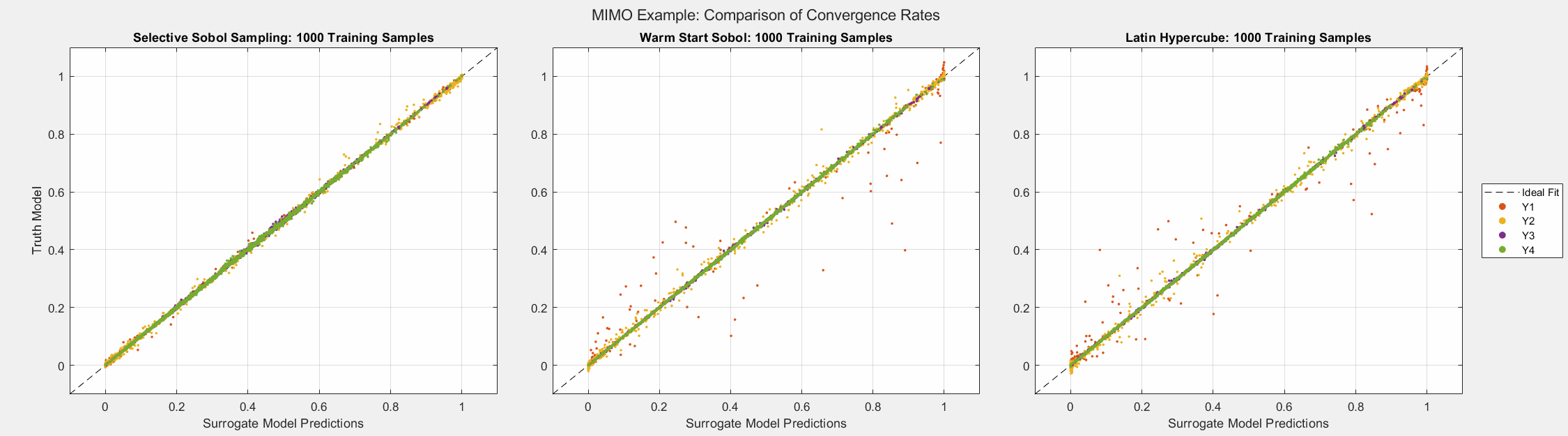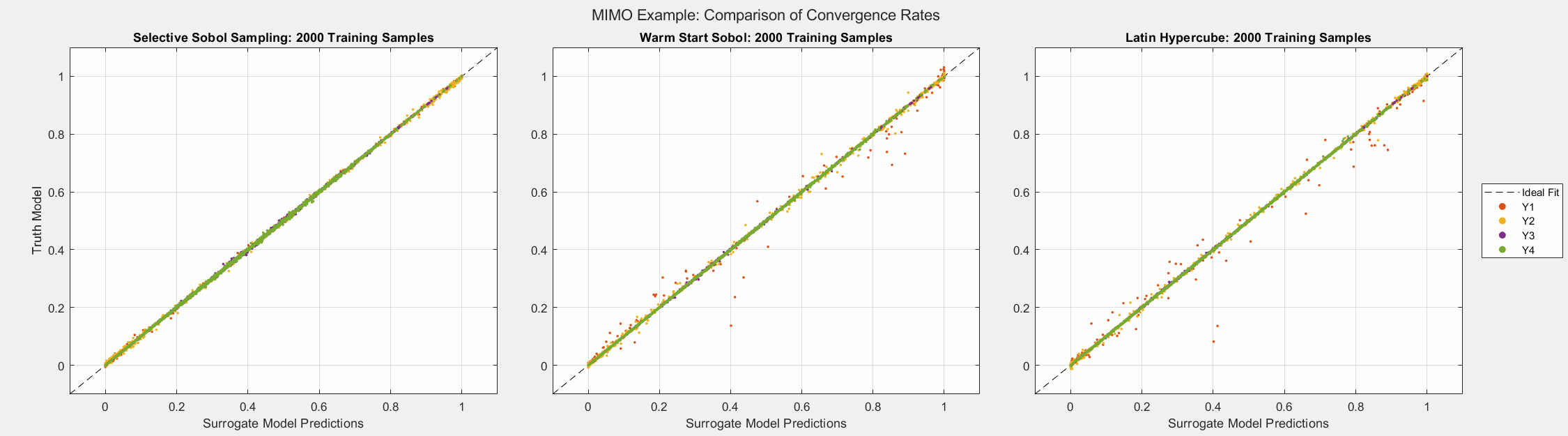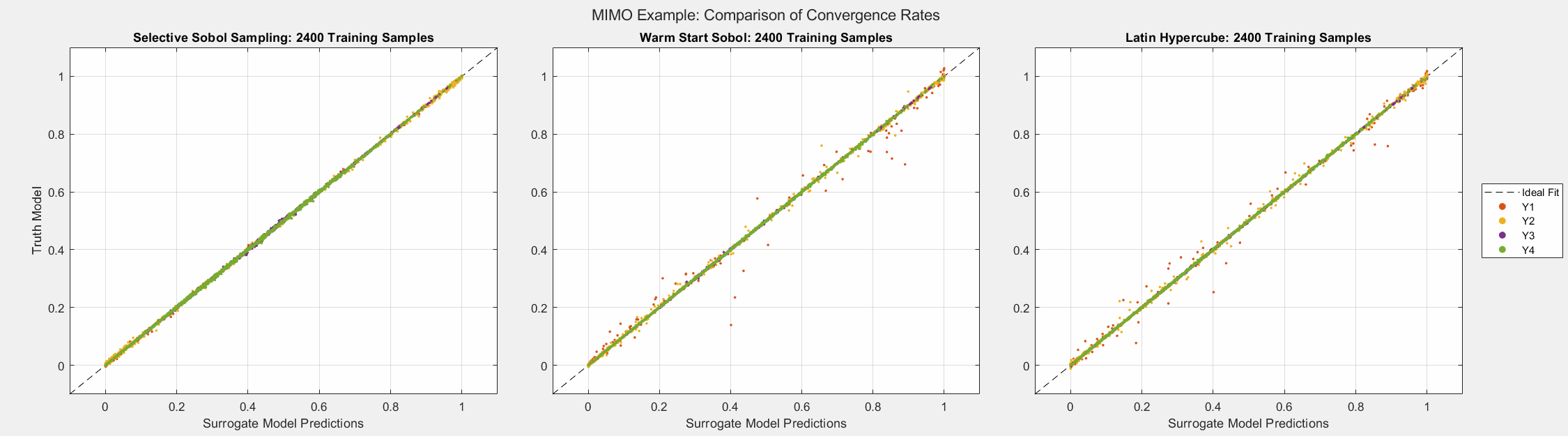
Multiple-Input Multiple-Output Example
In this example, we demonstrate that the benefits of SSS extend to systems with multiple inputs and outputs. We now consider the following set of equations:
\(y_1 = \bigg(1 + e^{-(3x_1 + 2.8x_2 – 5.0)(10 + 48 \sqrt{(x_1 – x_2)^2})} \bigg)^{-1}.\)
\(y_2 = \bigg(1 + e^{-(1.75x_1 + 2.85x_3 – 1.5)(6 + 12 \sqrt{(x_1 – x_3)^2})} \bigg)^{-1}.\)
\(y_3 = \frac{3x_2 + 1.5x_3 + 0.89x^2_2 + 3.7x^2_3 + 4.5x_2x_3}{13.5}.\)
\(y_4 = \frac{2.5x_1 + 4.5x_2 + 2.19y^2_3 + 6.7x^2_2 + 3.48x_1y_3}{19}.\)
\(y = [y_1, y_2, y_3, y_4].\)
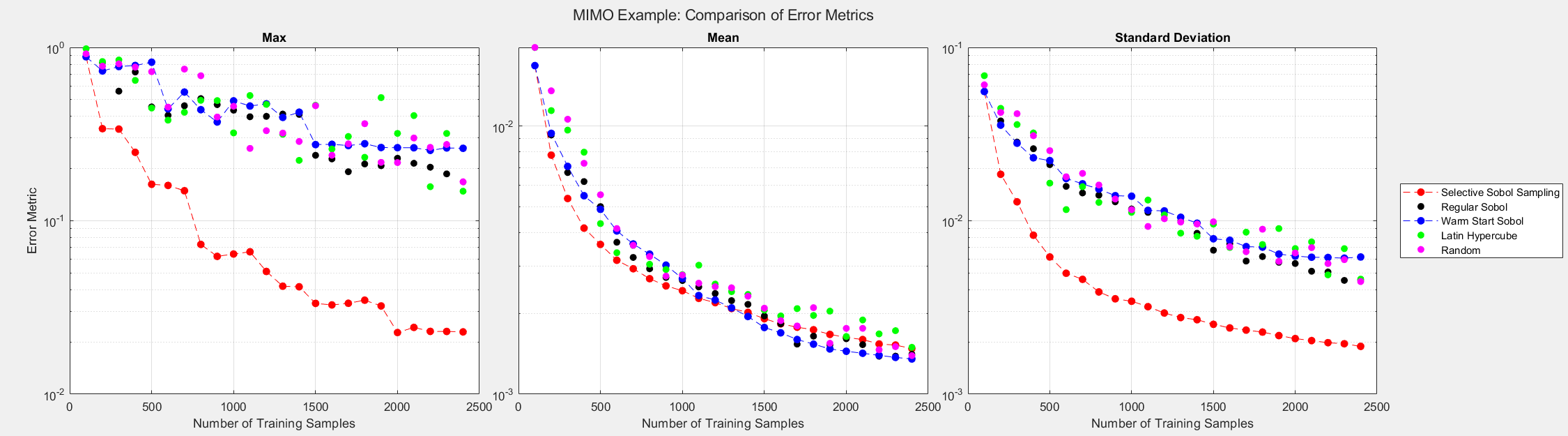
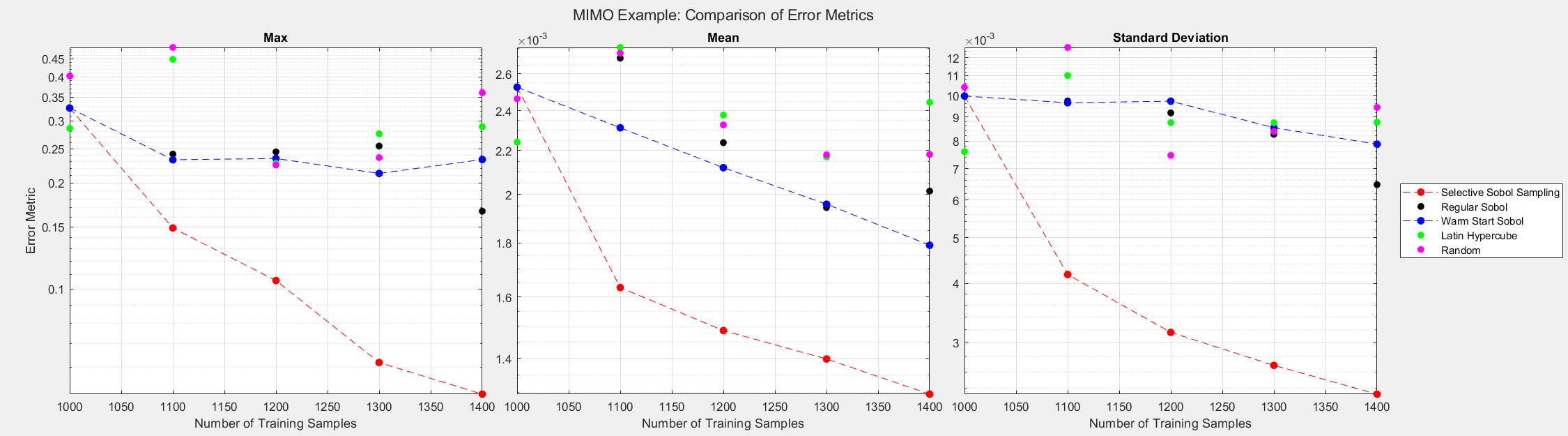
The equations were scaled such that the maximum of each output is near unity. The error metrics in the figure below are computed over all the outputs.
The figures below show the surrogate model’s convergence behavior using different sampling approaches. We used the same testing set (2000 samples) to evaluate all metrics presented. Warm start sampling approaches are displayed with dotted lines to indicate dependence on a previous model. Sample sets were incremented by 100. See the provided code for details on the model architecture and training methods.
As the plots below show, SSS outperforms all passive sampling methods and consistently reduces the error metrics as more samples are introduced. Note that even though the mean of the error seems comparable across all sampling methods, the animated figure shows that \(y_1\) and \(y_2\) converge much quicker and uniformly when the SSS algorithm is used.
Simple Example
A simple example is used to demonstrate that SSS and passive sampling methods perform similarly when the system produces outputs that are somewhat linear. Nevertheless, using SSS in these cases does not negatively impact the convergence or performance of the surrogate model. Suppose we represent a system with the following equation:
\(y = \frac{3x_1 + 1.5x_2 + 4.5x_1x_2}{9}.\)
The equation was scaled such that the maximum of the output is near unity.
The figure below shows the surrogate model’s convergence behavior when using different sampling approaches. We used the same testing set (2000 samples) to evaluate all metrics presented; see the associated code for details. Warm start sampling approaches are displayed with dotted lines to indicate dependence on a previous model. Sample sets were incremented by 100. See the provided code for details on the model architecture and training methods.
As seen in the plots below, the sampling methods perform similarly. Since the equation used does not result in skewed outputs, passive sampling methods produce a data set of similar quality to the one produced by SSS.
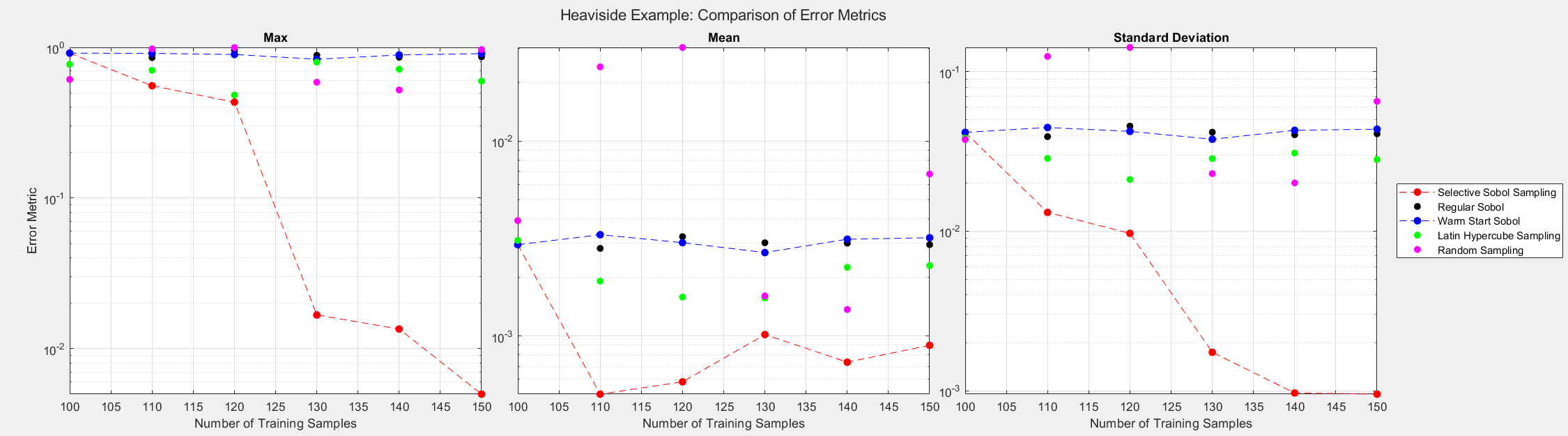
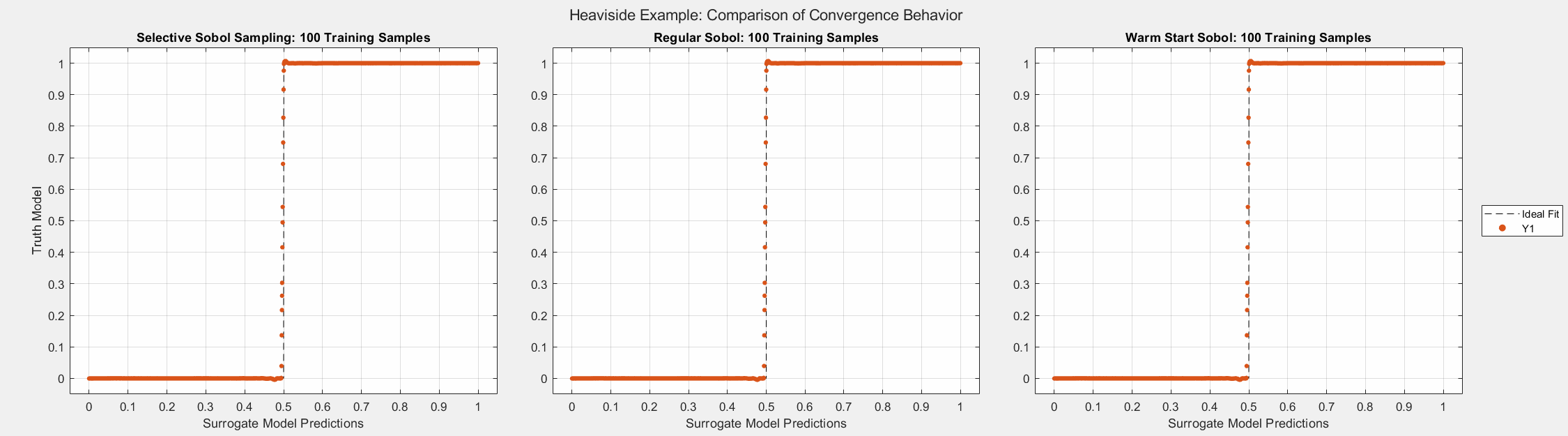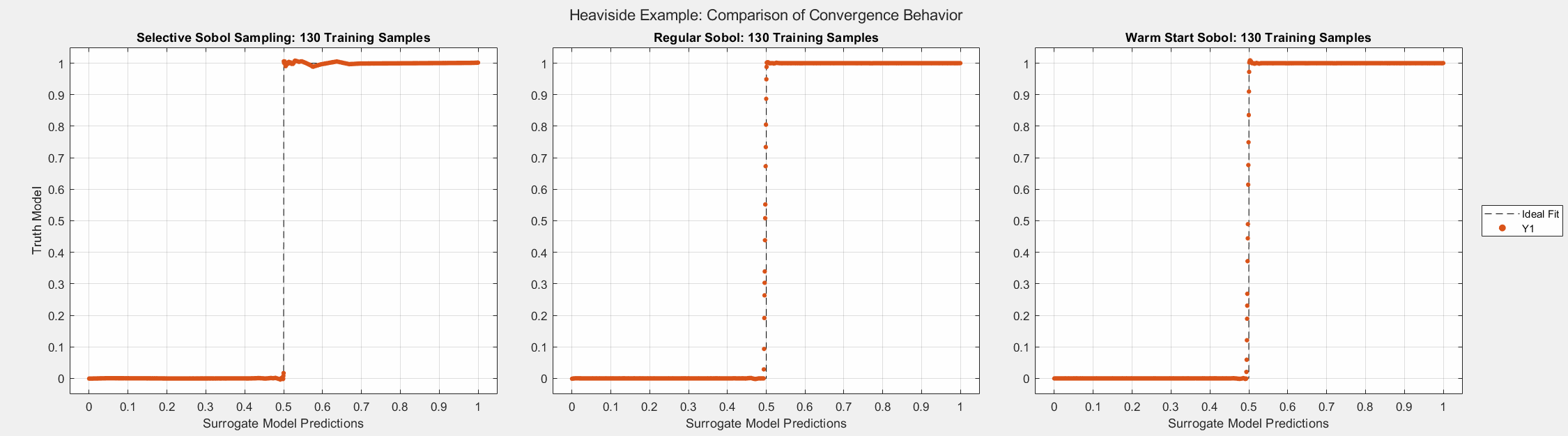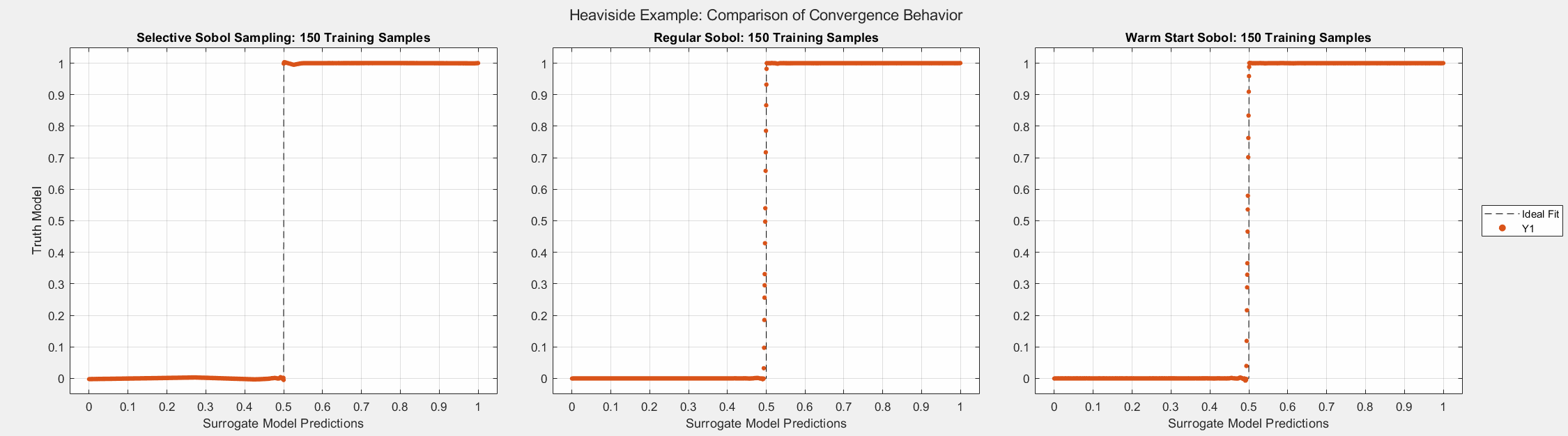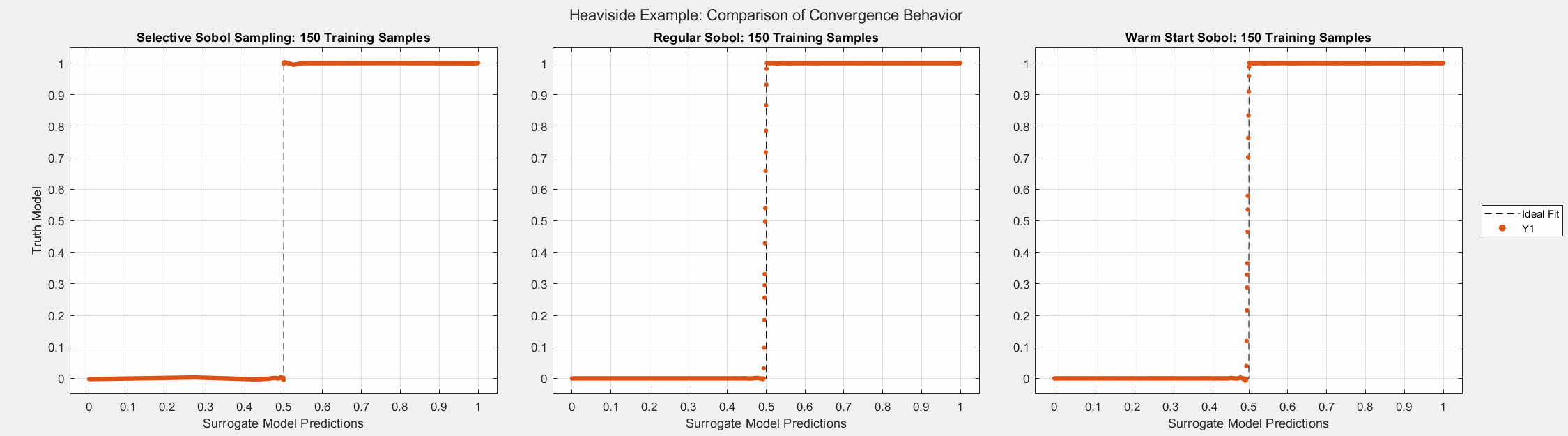
Heaviside Example
The final analytical example demonstrates that the SSS algorithm still performs well even when different inputs result in the same output, proving that the algorithm makes selections based on more than the value of outputs. For this experiment, we consider the Heaviside function given by:
\(
y =
\begin{cases}
0 & \text{if } x < 0.5 \\
1 & \text{if } x \geq 0.5
\end{cases}
\)
y =
\begin{cases}
0 & \text{if } x < 0.5 \\
1 & \text{if } x \geq 0.5
\end{cases}
\)
The figures below show the surrogate model’s convergence behavior when using different sampling approaches. We used the same testing set (2000 samples) to evaluate all metrics presented. Warm start sampling approaches are displayed with dotted lines to indicate dependence on a previous model. We used an initial training set of size 100 to train the initial models, and the training sets were then incremented by 10 for each additional round of training. See the provided code for details on the model architecture and training methods.
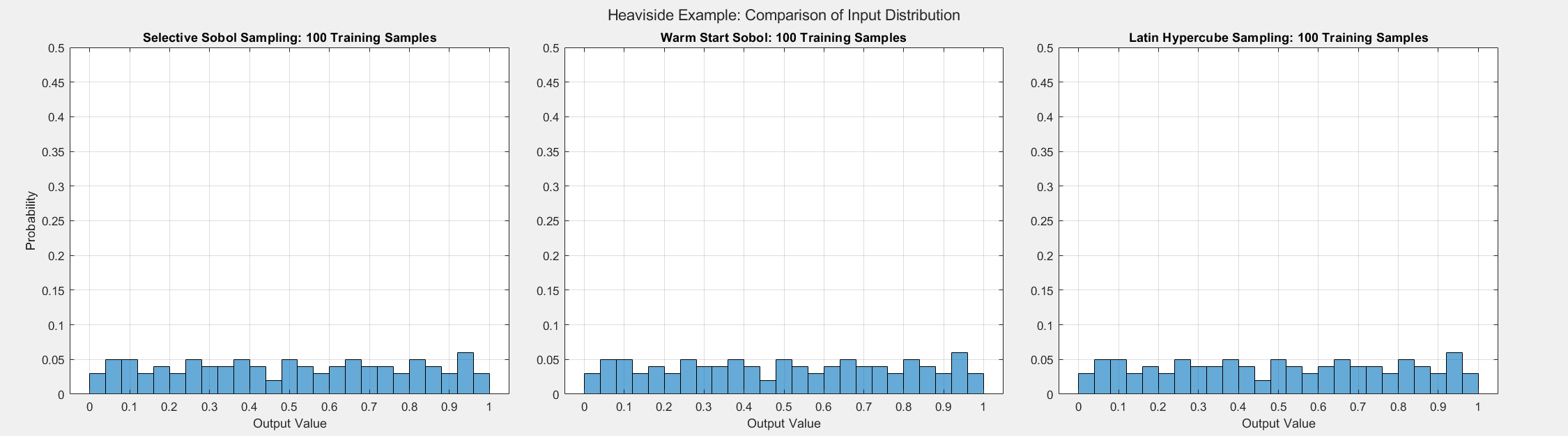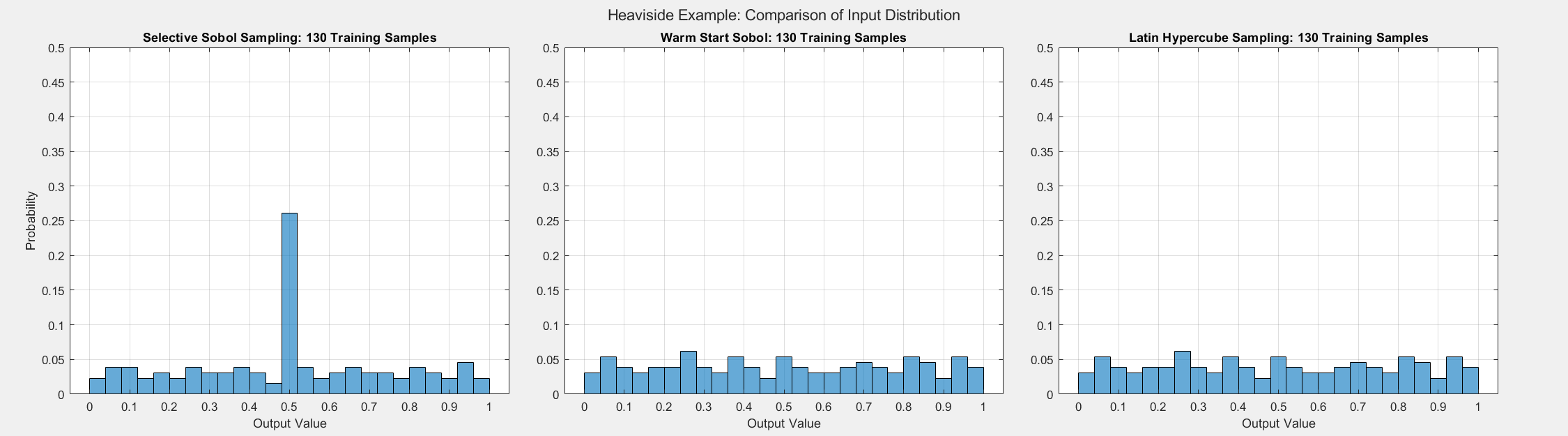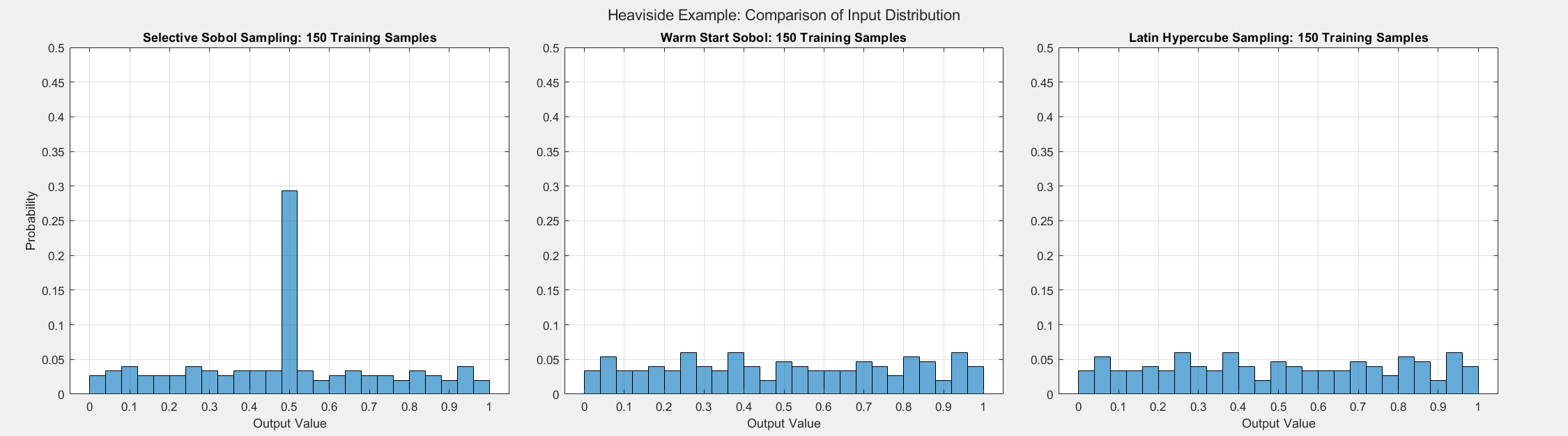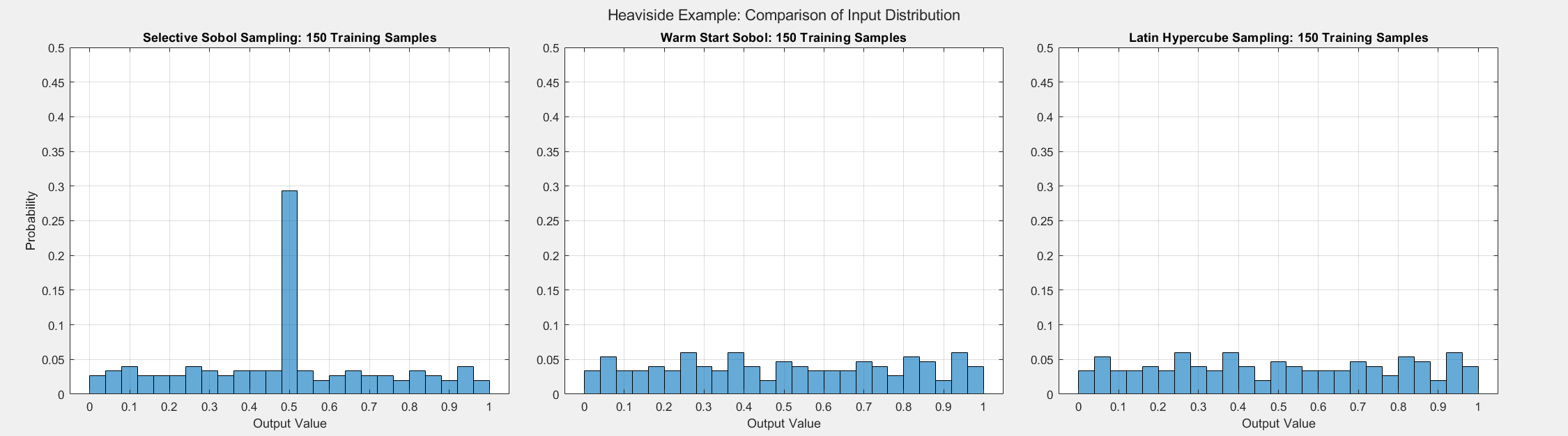
As the plots below show, SSS outperforms all passive sampling methods. Furthermore, comparing the distributions of input samples between different sampling methods reveals that SSS is actively seeking high-information regions.
DWSIM Example
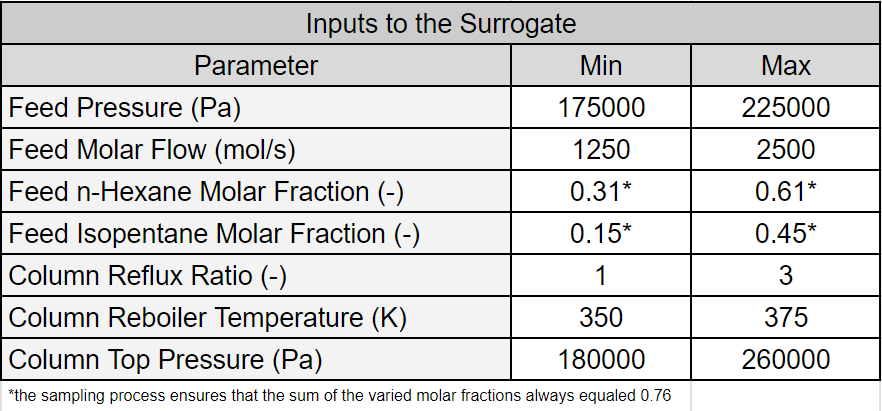
We adapted Example 1 from DWSIM Surrogate Creation. Input bounds were adjusted to highlight the difficulty of obtaining a well-fitted surrogate when input bounds are widened. Some output parameters were removed to reduce the result and plotting clutter. The first table lists the surrogate model inputs and their bounds. The second table below lists the output parameters and the minimum and maximum values in the testing data set.
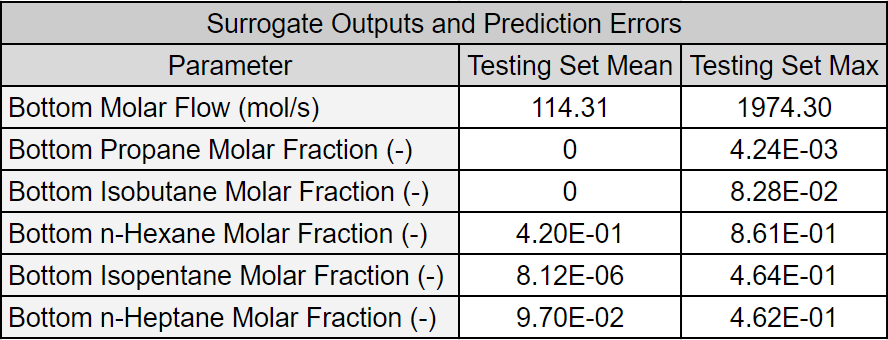
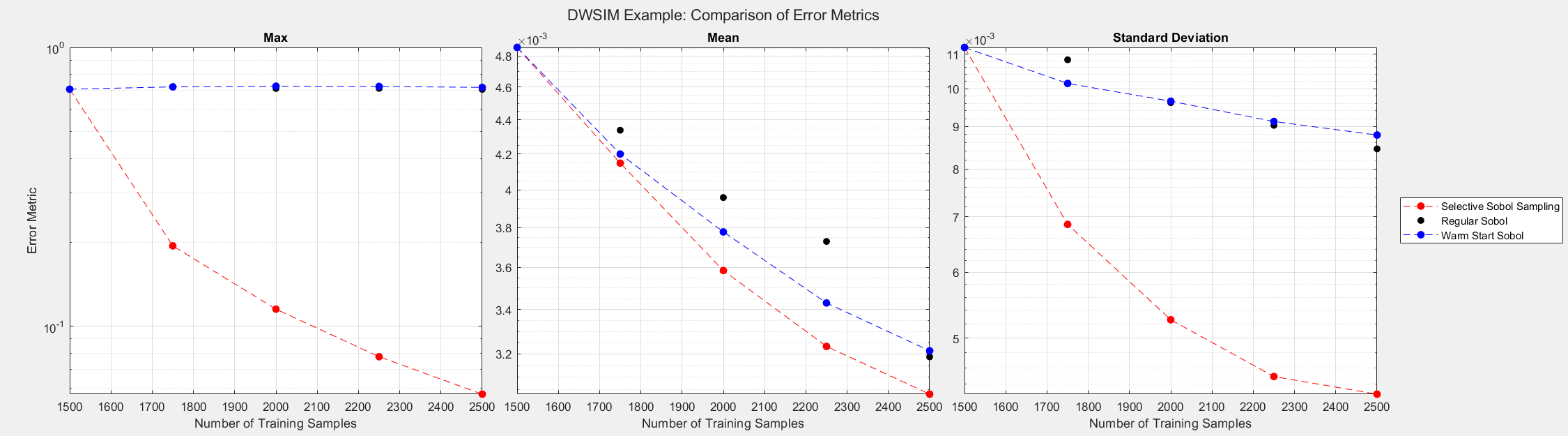
In the plots below, output parameters were min-max normalized to obtain a consistent comparison over all outputs. The plots show the surrogate model’s convergence behavior when using different sampling approaches. We used the same testing set (2000 samples) to evaluate all metrics presented; see the associated code for details. Warm start sampling approaches are displayed with dotted lines to indicate dependence on a previous model.
For this experiment, we only tested the Sobol sampling methods. We used an initial training set of size 1500 to train the initial models, and the training sets were then incremented by 250 for each additional round of training. See the provided code for details on the model architecture and training methods.
SSS reduced the error metrics far better than the other methods as more samples were added to the training set.
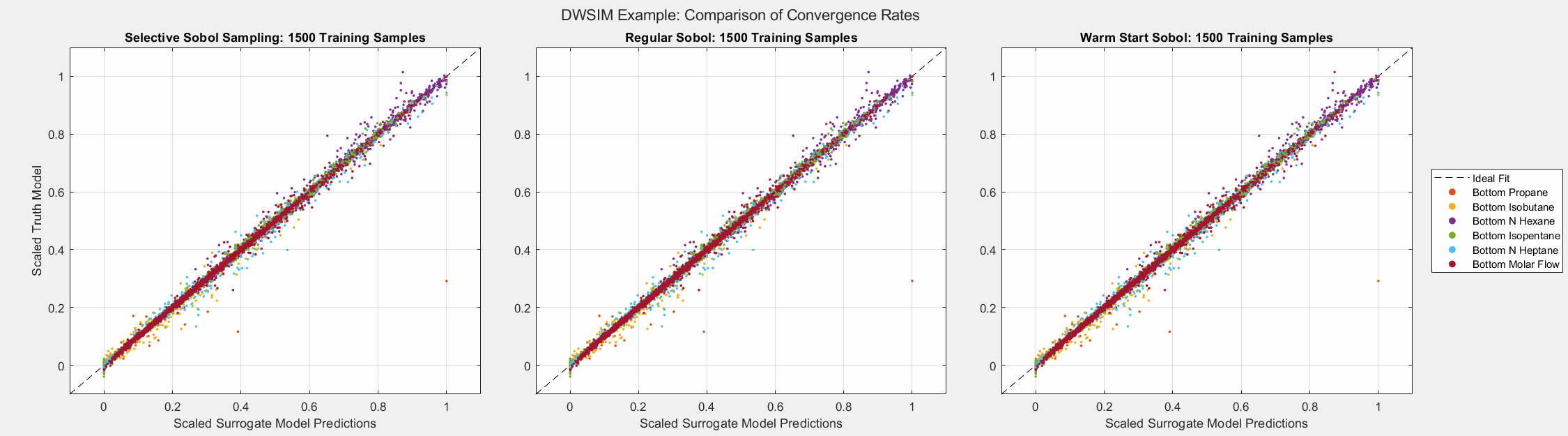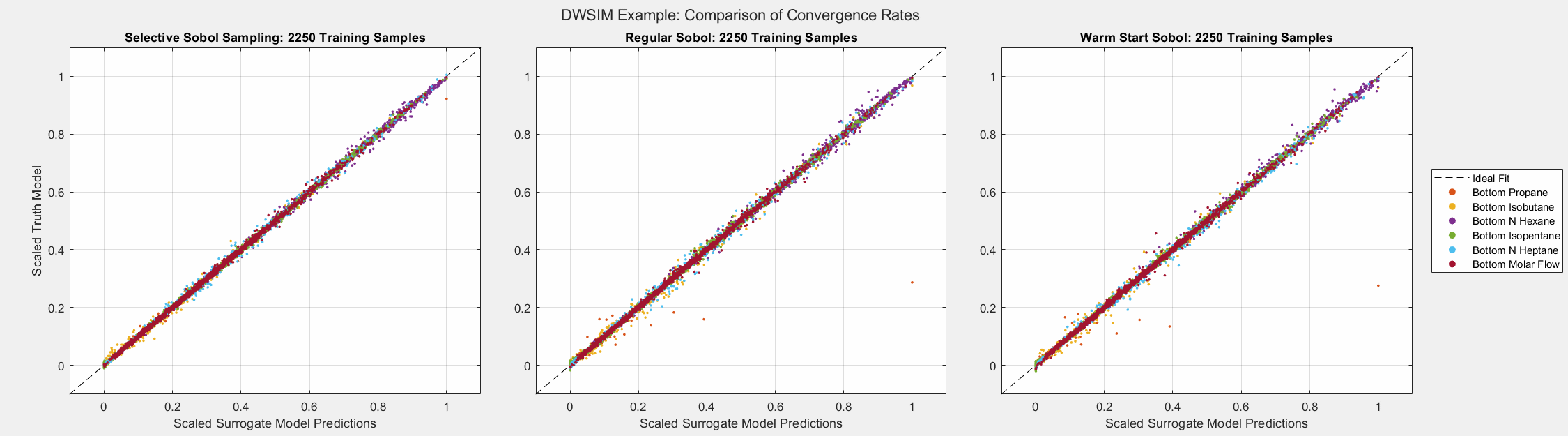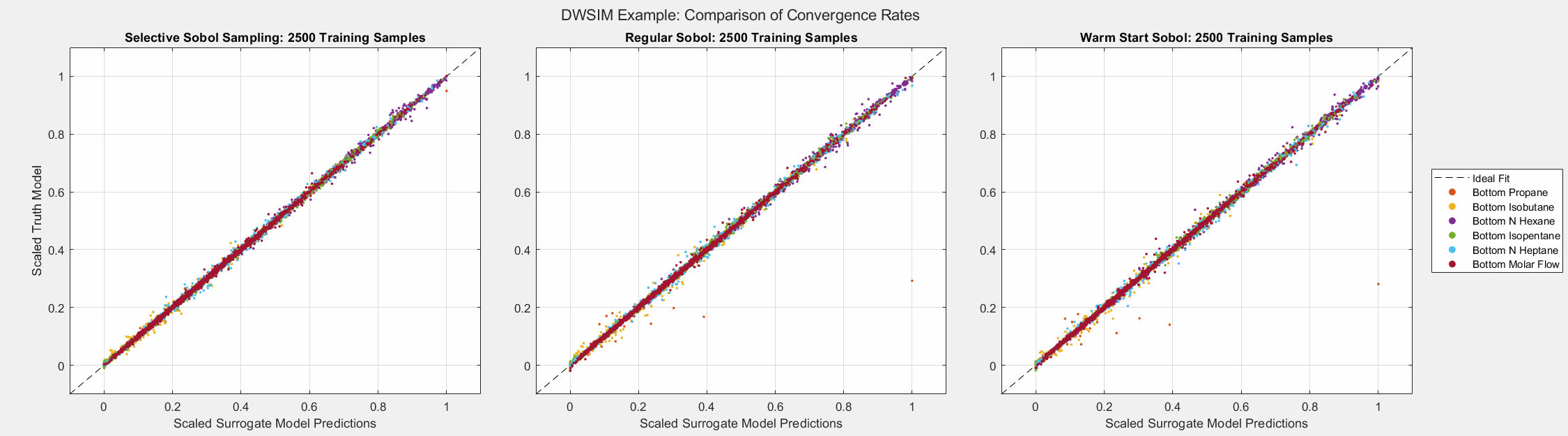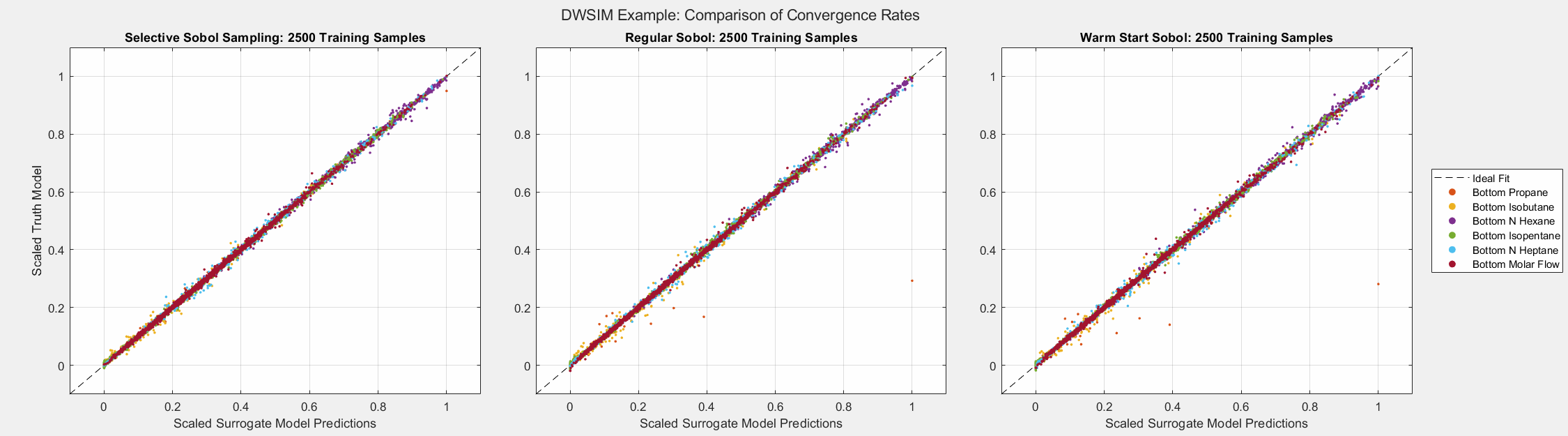
The animated figures below display the convergence behavior of all three Sobol sampling methods used in this experiment. The first figure displays all predicted outputs, while the second only shows the propane molar fraction. Note that SSS dramatically increased the accuracy of the model’s prediction of the propane molar fraction, especially when the parameter is larger than average. As shown in the final plot, this parameter tends to be small in most cases. Given the bounds of the input parameters and the system’s behavior, there are some instances when this parameter can be larger than usual. A surrogate model must be able to capture the complete behavior of the system even when some behavior is unusual. This very behavior of distillation columns motivated us to develop Selective Sobol Sampling.
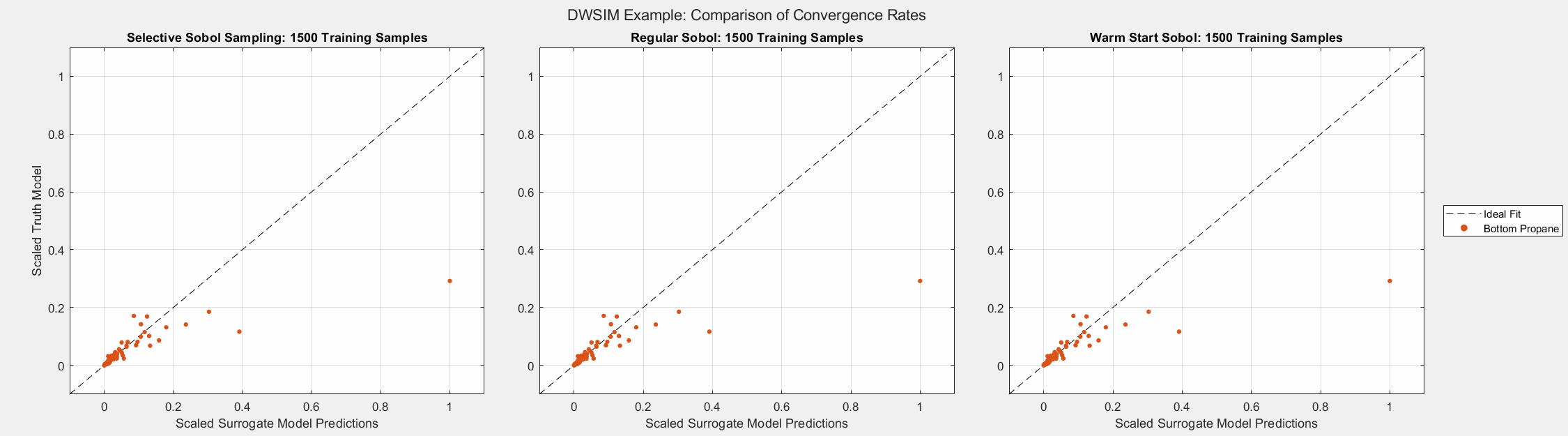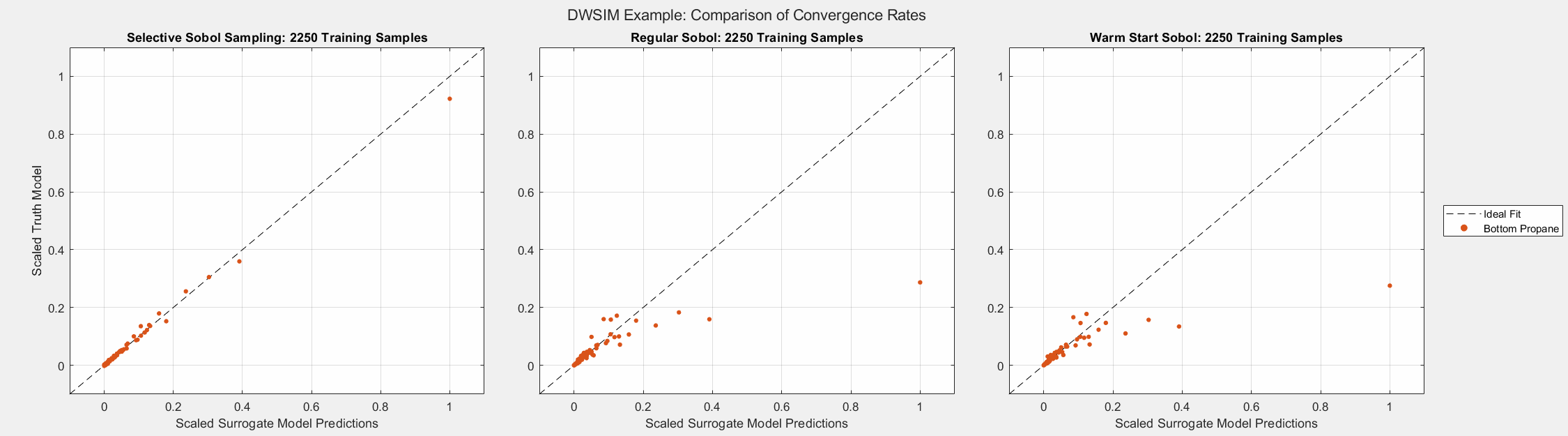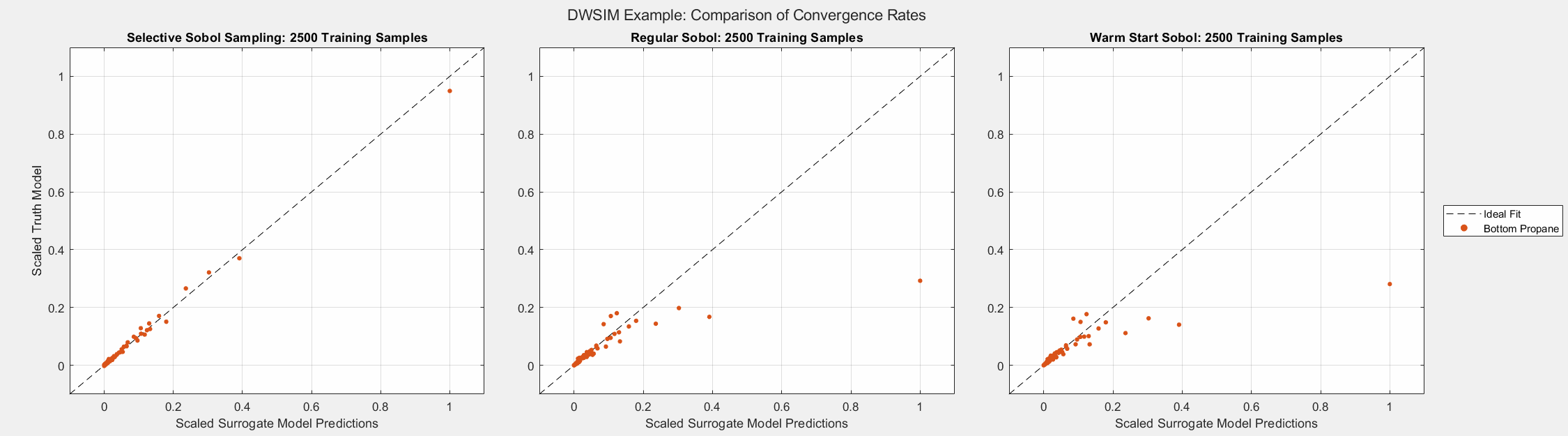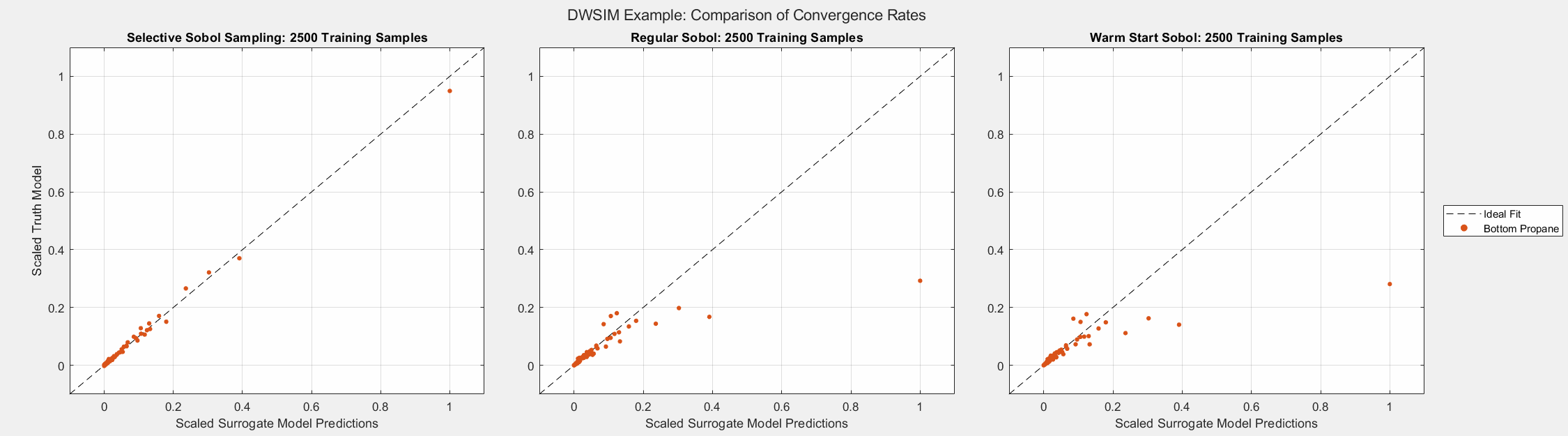
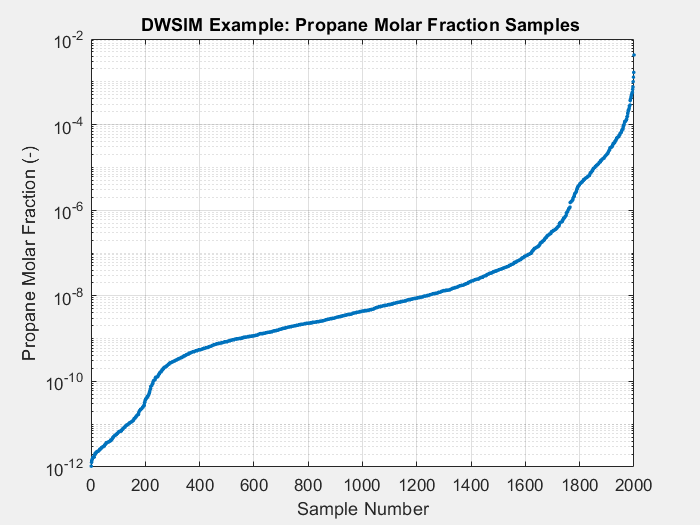
Algorithm’s Computation Effort
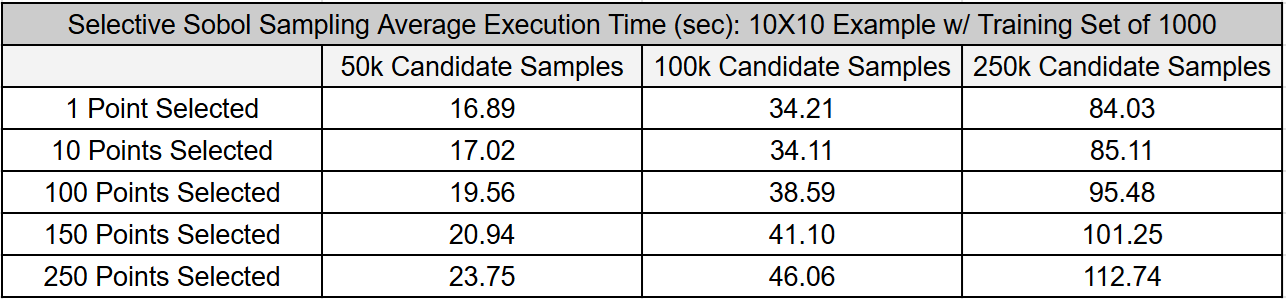
The tables below present the average time required to execute the Selective Sobol Sampling task for two surrogate model architectures. We conducted these experiments on a laptop with an Intel i9-11900H processor (2.50 GHz). We assumed a surrogate model trained with 1000 samples was already available in both cases. The numbers presented are the averages of 200 executions.
While the execution time is influenced by the number of points selected and the size of the candidate pool, it’s crucial to note that the majority of the computational effort is concentrated on the first point. Subsequent points require significantly less effort. The computational effort of the Selective Sobol Sampling algorithm, implemented in Matlab using a single thread, can be reduced through parallelized approaches.
Overall, the computational effort for the Selective Sobol Sampling algorithm is relatively tiny compared to its benefits. This is particularly evident in the DWSIM case, where adding 1000 samples resulted in only marginal performance improvements unless the Selective Sobol Sampling method was used.
The first table presents results from the motivating example discussed earlier. The second table extends this example to include ten inputs and ten outputs, illustrating the effect of input and output size on execution time.
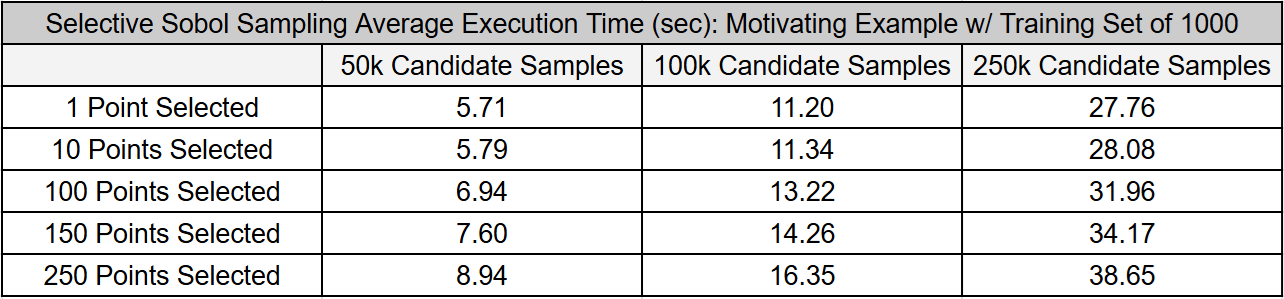
Expanding an Existing Set
In the analytical examples above, we used the Selective Sobol Sampling method throughout the training process. However, in some cases, it might be more efficient to use Selective Sobol Sampling only when necessary, avoiding the computational cost of training several surrogate models.
The figure below shows a variation of the Multiple-Input Multiple-Output example. We used an initial training set of size 1000 to train the initial models. Assume that the initial surrogate model did not meet exit criteria (testing metrics were too high) and more samples were needed to reduce the prediction error. The figure below shows the comparison between sampling methods. Sample sets were incremented by 100 points before retraining. Notably, the SSS method significantly reduces error faster than other methods and requires training far fewer surrogate models than the original experiment.
Other Variations
- Expanding Input Bounds: The algorithm can be adapted when input bounds need to be adjusted for an existing surrogate model. The existing data set and selected inputs do not need to have the same bounds.
- Additional Inputs: The method can be adapted to introduce an additional input to an existing model, preventing unnecessary resampling if additional parameters or inputs are needed as a workflow evolves.
- Continuous Learning: The diagram above can be modified so that model sampling and surrogate training occur concurrently, reducing the time to obtain a well-fitted surrogate model.
Summary
The article introduces Selective Sobol Sampling (SSS), an algorithm that actively leverages existing data and previously trained models to select the most informative samples, improving predictive accuracy and reducing training time. Unlike conventional methods like Latin Hypercube and Sobol sampling, which passively generate samples, SSS ranks potential inputs based on the current data set and surrogate model. Analytical examples demonstrate that SSS consistently outperforms passive sampling methods, particularly in capturing nonlinear behaviors. Furthermore, a DWSIM example shows that SSS is useful in practical situations.
References
[1] Iman, R L, Davenport, J M, and Zeigler, D K. Latin hypercube sampling (program user’s guide). [LHC, in FORTRAN]. United States: N. p., 1980. Web.
[3] Renardy, Marissa et al. “To Sobol or not to Sobol? The effects of sampling schemes in systems biology applications.” Mathematical biosciences vol. 337 (2021): 108593. doi:10.1016/j.mbs.2021.108593